2022年国考行测数量之《巧用分步法解概率“两人相邻”问题》磐石华图

2022年国考行测数量之《巧用分步法解概率“两人相邻”问题》磐石华图

　　行测考试中，概率问题是考试的重点，也是拉开分数的关键题型，但是，有些概率题相对比较复杂，如果按部就班的解，可能会耗费很多的精力和时间，还有可能出现计算错误，所以，如何快速、精准解题成为考试关键。接下来给大家梳理一下概率问题中的一种典型问题，即“两人相邻”的类型题。

　　我们先看一个典型的题目：

　　【例1】某次圆桌会议共设8个座位，有4个部门参加，每个部门2人，排座位时，要求同一部门的两人相邻，若小李和小王代表不同部门参加会议，则他们座位相邻的概率是：

　　【答案】D

　　【解析】如果用正常思路去解，利用公式：概率=满足的情况数÷总情况数。总情况数使用捆绑法，4个部门看成4个整体进行环形排列，每个部门内部排序，根据环形排列公式，n个人环形排列的方式有

　　【解析】如果用正常思路去解，利用公式：概率=满足的情况数÷总情况数。总情况数使用捆绑法，4个部门看成4个整体进行环形排列，每个部门内部排序，根据环形排列公式，n个人环形排列的方式有。满足要求的情况为小李和小王所在部门挨着且相邻的是这两人，这两个部门的排列只有小李同事+小李+小王+小王同事，或者小王同事+小王+小李+小李同事两种情况，再与其他两个部门一起环形排列，有2×种方式。则所求概率为两者相除，约分为。因此，选择D选项。

　　。满足要求的情况为小李和小王所在部门挨着且相邻的是这两人，这两个部门的排列只有小李同事+小李+小王+小王同事，或者小王同事+小王+小李+小李同事两种情况，再与其他两个部门一起环形排列，有2×

　　【解析】如果用正常思路去解，利用公式：概率=满足的情况数÷总情况数。总情况数使用捆绑法，4个部门看成4个整体进行环形排列，每个部门内部排序，根据环形排列公式，n个人环形排列的方式有。满足要求的情况为小李和小王所在部门挨着且相邻的是这两人，这两个部门的排列只有小李同事+小李+小王+小王同事，或者小王同事+小王+小李+小李同事两种情况，再与其他两个部门一起环形排列，有2×种方式。则所求概率为两者相除，约分为。因此，选择D选项。

　　种方式。则所求概率为两者相除，约分为

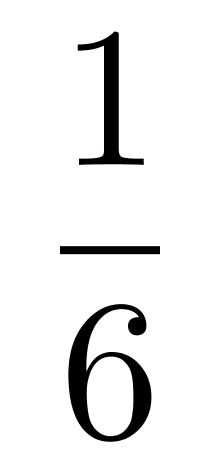
　　【解析】如果用正常思路去解，利用公式：概率=满足的情况数÷总情况数。总情况数使用捆绑法，4个部门看成4个整体进行环形排列，每个部门内部排序，根据环形排列公式，n个人环形排列的方式有。满足要求的情况为小李和小王所在部门挨着且相邻的是这两人，这两个部门的排列只有小李同事+小李+小王+小王同事，或者小王同事+小王+小李+小李同事两种情况，再与其他两个部门一起环形排列，有2×种方式。则所求概率为两者相除，约分为。因此，选择D选项。

　　。因此，选择D选项。

　　但是，我们会发现，这种解法明显比较杂，而且计算量还比较大，容易出错，所以我们采用另一种思维：先排小李，再排小王。

　　解法：使用分步概率，先让小李和小王中的一个人随机选择座位，概率是1;这个人选择完之后他的部门同事也跟着占去他左边或者右边的一个座位，那么还剩下6个座位，只有1个座位能跟第一个人挨着，第二个人选择的概率是，分步用乘法，小李小王相邻的概率为

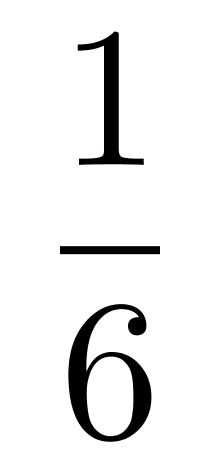
　　解法：使用分步概率，先让小李和小王中的一个人随机选择座位，概率是1;这个人选择完之后他的部门同事也跟着占去他左边或者右边的一个座位，那么还剩下6个座位，只有1个座位能跟第一个人挨着，第二个人选择的概率是，分步用乘法，小李小王相邻的概率为。

　　我们会发现，解题明显变得简单得多，而且准确大大提高，这就是利用了概率当中的分步计算。我们再来看两个例题。

　　【例2】小张和小王在同一个学校读研究生，每天早上从宿舍到学校有6:40、7:00、7:20和7:40发车的4班校车。某星期周一到周三，小张和小王都坐班车去学校，且每个人在3天中乘坐的班车发车时间都不同。问这3天小张和小王每天都乘坐同一趟班车的概率在：

　　A.3%以下

　　B.3%~4%之间

　　C.4%~5%之间

　　D.5%以上

　　【答案】C

　　【解析】我们用分步的思维去解题，要使两人车次相同，小张任意选择，小王选择与小张一样的即可。第一天小张任意选，概率为1，小王在四个选择中只能选择与小张一致的，4选1，概率为

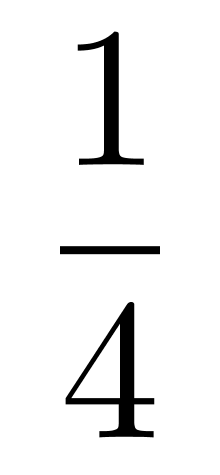
　　【解析】我们用分步的思维去解题，要使两人车次相同，小张任意选择，小王选择与小张一样的即可。第一天小张任意选，概率为1，小王在四个选择中只能选择与小张一致的，4选1，概率为;同理，第二天小张任意选，概率为1，每天的发车时间都不同，小王3选1，概率为1/3;同理，第三天小张概率为1，小王概率为1/2。总概率为：。因此，选择C选项。

　　;同理，第二天小张任意选，概率为1，每天的发车时间都不同，小王3选1，概率为1/3;同理，第三天小张概率为1，小王概率为1/2。总概率为：

　　【解析】我们用分步的思维去解题，要使两人车次相同，小张任意选择，小王选择与小张一样的即可。第一天小张任意选，概率为1，小王在四个选择中只能选择与小张一致的，4选1，概率为;同理，第二天小张任意选，概率为1，每天的发车时间都不同，小王3选1，概率为1/3;同理，第三天小张概率为1，小王概率为1/2。总概率为：。因此，选择C选项。

　　。因此，选择C选项。

　　【例3】两个大人带四个孩子去坐只有六个位置的圆型旋转木马，那么两个大人不相邻的概率为：

　　【答案】B

　　要求两个大人不相邻，则让四个孩子先坐好，第一个大人先坐，概率为1，第一个大人坐好和4个孩子形成5个空位，第二个大人可以坐这5个位置的任意一个，只有坐在不相邻的3个时候两个大人不相邻，因此两个大人不相邻的概率为3/5。因此，选择B选项

　　通过几个题的练习，相信大家对分步解概率题有了一定的概念，在以后的做题中，一定要活学活用，提高解题效率。

以上就是【2022年国考行测数量之《巧用分步法解概率“两人相邻”问题》磐石华图】的相关介绍，如果要了解更多热门资讯，欢迎关注吉林华图教育。