2022-03-25 14:12:39 吉林公务员考试网 jl.huatu.com 文章来源:华图教育
数量中一元二次方程和均值不等式的应用
2021年山西省考数量关系题目由往年的10道题增加到了15道题目,题量的增加也显示出了在公考过程中对数学思维考查的重视程度,结合近年来进面分值要求越来越高,如果考试时完全放弃数量关系题目,就很难拿到一个高分数,也就无法为成功上岸打下良好的基础。而数量关系之所以难,原因之一是因其题目综合性强,对考生逻辑思维能力要求较高,但是数量虽难,很多题目却有着比较强的技巧性,而且一些知识点也在历年的考试题目当中多次出现,所以如果我们可以学习并掌握这些题目,就能在短时间内求解出这类题目。其中,最值问题便是省考中与其他类型考点结合考查频率较高的一类,例如几何求最值,经济利润问题求最值,都用到了相应的最值理论,接下来小编就对最值问题进行论述,希望对各位同学有所帮助。
理论知识
![]()
1.一元二次方程求最值的应用:,(1)当a>0时,y在处取得最小值;(2)当a<0时,y在处取得最大值。
![]()
2.均值不等式理论的应用:a+b≥2(a、b均为正整数,当且仅当a=b时等号成立)。
![]()
依据均值不等式,可得对于一个矩形而言,(1)周长C一定时,面积S取得最大值,;(2)面积S一定时,周长C取得最小值,。
解题思路与技巧
观察题目设问方式,求最大或最小且涉及上述理论知识当中的哪一个,确定后套用公式即可。
例题精讲
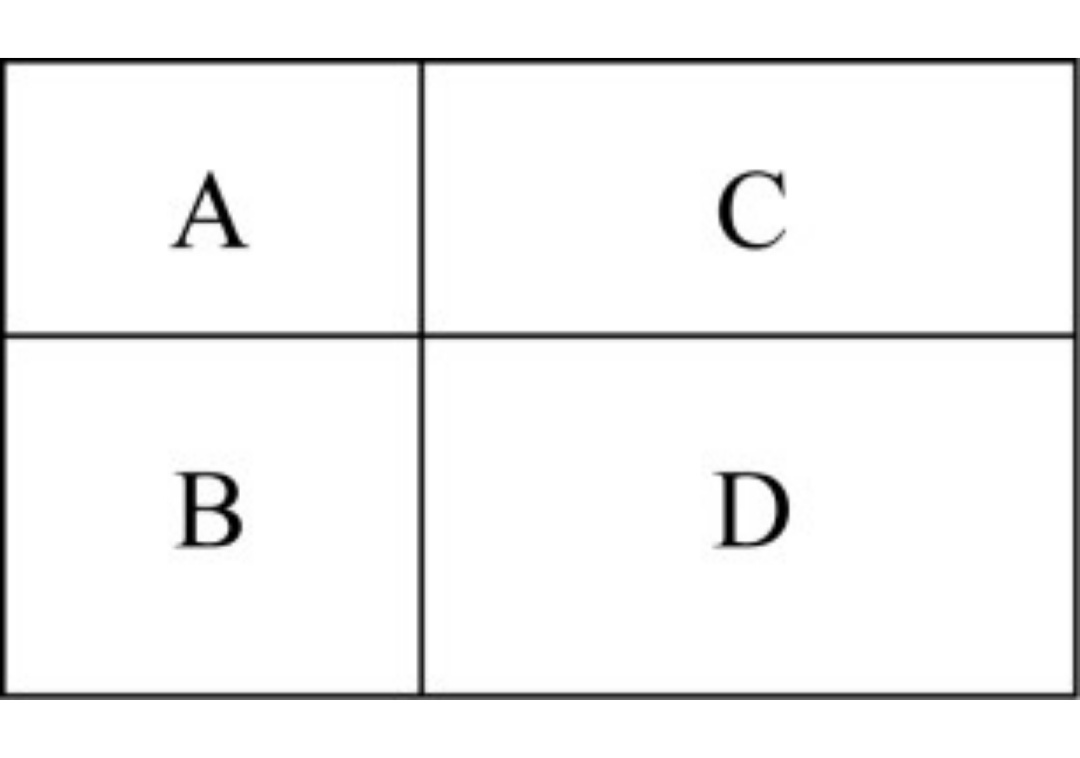
【例1】(2020年联考)村民陶某承包一块长方形种植地,他将地分割成如图所示的4个小长方形,在A、B、C、D四块长方形土地上分别种植西瓜、花生、地瓜、水稻。其中长方形A、B、C的周长分别是20米、24米、28米,那么长方形D的最大面积是:
A.42平方米B.49平方米
C.64平方米D.81平方米
【答案】C
【解析】第一步,本题考查几何最值问题。
第二步,设A的长宽分别为a、b,则a+b=10,B与A长相同,设其宽为c,则a+c=12,C与A宽相同,设其长为d,则b+d=14,D与B宽相同,与C长相同,则c+d=(a+c)+(b+d)-(a+b)=12+14-10=16,则D周长为32。
![]()
第三步,由均值不等式可得,当周长一定时,面积取得最大值。
因此,选择C选项。
【例2】(2019年深圳)某类商品按质量分为8个档次,最低档次商品每件可获利8元,每提高一个档次,则每件商品的利润增加2元。最低档次商品每天可产出60件,每提高一个档次,则日产量减少5件。若只生产其中某一档次的商品,则每天能获得的最大利润是()元。
A.620B.630
C.640D.650
【答案】C
【解析】第一步,经济利润问题最值优化类。
![]()
第二步,设提升了n个档次,总利润为y,根据总利润=每件商品的利润×销售量,可得,令y=0,解得n1=-4,n2=12,当时,y取得最大值。
第三步,y最大值=(8+2×4)×(60-5×4)=640元。
因此,选择C选项。
根据例题2可以看出通常情况如果将y值写成两个数相乘的形式,这样不需要再记住对称轴公式,相对更容易求解,节省时间。
综上可以看出,经济利润问题最值优化类以及几何问题求最值常常是与函数问题相结合,因此,只要大家掌握了函数求最值的相应技巧,这类问题便可迎刃而解!
以上就是【数量中一元二次方程和均值不等式的应用】的相关介绍,如果要了解更多热门资讯,欢迎关注吉林华图教育。

贴心微信客服