“隔板法”巧解公务员考试行测同素分堆问题

“隔板法”巧解公务员考试行测同素分堆问题

　　排列组合在行测数量关系中考的比较多，相对来说也是难度较高的一类题型。而其中有一类相同元素分堆的问题，如果用分类分步的思路去求解会比较麻烦，今天就带大家用“隔板法”来解决这类问题。

　　概念了解

　　同素分堆：按照要求将同种元素进行不同分堆，有多少种分配方式。

　　使用条件

　　1.同种元素分堆;

　　2.每堆“至少一个”。

　　3.元素全部分完。

　　解题思路

　　例1

　　将10个大小相同苹果分配给3个小朋友，每人至少一个，有多少种分配方式?

　　A.36 B.72 C.120 D.720

　　【答案】A。解析：10个苹果是一样的，把它分给3个小朋友，“每人至少一个”。那我们可以将10个苹果放成一排，用2个板将其隔开，就可以分成3份。如图所示：

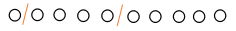
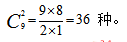
　　此时我们发现10个苹果之间形成9个空，在这些空里插入2个隔板即可，那插入的位置不同，苹果就会被分成不同的3份，即分配的方式为9个位置选2个有

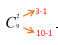
　　总结：由可得，将n个相同元素分给m个不同的对象，每个对象至少一个元素的情况数有即隔板法。

　　例2

　　将10个大小相同苹果分配给3个小朋友，每人至少两个，有多少种分配方式?

　　A.15 B.20 C.25 D.30

　　【答案】A。解析：10个苹果分给3个小朋友，要求每人至少两个，用隔板法解题时，需要将条件“每人至少两个”转化为“每人至少一个”才可以。

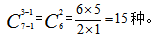
　　由于苹果一样，要求“每人至少两个”，那我们就可以先从总数中拿出3个，先分给每人1个，此时每人手里已有1个苹果，那么再分配剩余7个苹果时，只要保证“每人至少一个”就能最终保证“每人至少两个”。此时问题就变成了“7个苹果分给3个小朋友，每人至少一个，共有多少积分法?”利用隔板模型公式得：

　　例3

　　将10个大小相同苹果分配给3个小朋友，随意分配，有多少种分配方式?

　　A.36 B.56 C.66 D.76

　　【答案】C。解析：10个苹果分给3人，此时随意分，那也就是说有人可能分到0个，不满足隔板法的使用条件。此时要想使用隔板法快速解题，就需要将条件“随意分配”转化为“至少一个”。

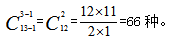
　　那么要求“随意分配”时，我们就可以让每人先“借给”总数1个，再按“每人至少一个”分配时就相当于又还给了每个人，这时就可以用隔板模型了。每个小朋友“借给”总数1个苹果，总数就会变成13个苹果。此时题目就变成了“13个苹果分给3个小朋友，每人至少一个，共有多少种分法?”利用隔板模型公式得：

　　总结：通过例2和例3可以发现，要分相同元素给不同对象但题干条件不满足的情况下，可以通过“先分”和“先借”将题干条件转化为“每个对象至少一个”，进而用隔板模型解决。

　　了解完隔板模型的解题方法后，相信大家就会发现这类特殊的排列组合题目也可以快速掌握并有效解决，望各位考生备考时打好坚实的基础，灵活使用各种方法，祝各位考生取得优异的成绩。

以上就是【“隔板法”巧解公务员考试行测同素分堆问题】的相关介绍，如果要了解更多热门资讯，欢迎关注吉林华图教育。