2022-02-08 09:20:08 军队人才网 jl.huatu.com/jzg 文章来源:未知
几何是研究形的科学,是以人们的视觉思维为主导,培养人的观察能力、空间想象能力和洞察力。随着工农业生产和科学技术的不断发展,几何学的应用越来越丰富,行政能力测试中考查的也越来越多,迎来了必考科目的大潮。
在具体行测考试中,几何考查内容涉及几何计算、几何特性和几何构造等方面。不管分析什么题目,我们都必须把基础几何图形的相关关系把握清楚。这样,出现基础计算之外的构造类图形我们才有思路进一步分析。就拿几何问题中平面图形梯形来举例,梯形一般主要涉及周长、面积的考查,但是,这一平面图形有时也会跟立体几何结合分析体积。下面我们通过两个题目来了解这一关系。
【例1】某社区拟对一块梯形活动场地进行扩建,经测算,如果将梯形的上底边增加1米,下底边增加1米,则面积将扩大10平方米;如果将梯形的上底边增加1倍,下底边增加1米,则面积将扩大55平方米;如果将上底边增加1米,下底边增加1倍,则面积将扩大105平方米。现拟将梯形的上底边增加1倍还多2米,下底边增加3倍还多4米,则面积将扩大多少?
A.280平方米
B.380平方米
C.420平方米
D.480平方米
【华图分析】
第一步,本题考查几何问题,属于平面几何类。
第二步,设梯形的上底、下底、高分别为a、b、h,根据“面积将扩大10平方米”可得,解得h=10(米);根据“面积将扩大55平方米”可得,解得a=10(米);根据“面积将扩大105平方米”可得,解得b=20(米)。
第三步,如果上底增加1倍多2米变为22米,下底边增加3倍多4米变为84米,则面积将扩大(平方米)。
因此,选择B选项。
【例2】某水渠长100米,截面为等腰梯形,其中渠面宽2米,渠底宽1米,渠深2米。因突降暴雨,水深由1米涨至1.8米。则水渠水量增加了:
A.112立方米
B.136立方米
C.272立方米
D.324立方米
【华图分析】
第一步,本题考查几何问题,属于立体几何类。
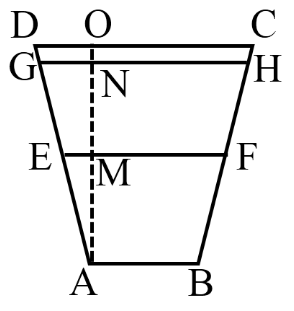
第二步,根据题意画出水渠的的截面图,见上图,其中EF为暴雨前水位线,GH为暴雨后水位线。由此可知,AB=1,CD=2,AM=1,可推知,那么。根据△AEM与△AGN相似,可知,即,解得GN=0.45,则GH=1+0.45+0.45=1.9。
第三步,水渠水量增加的体积为(立方米)。
因此,选择B选项。
通过这两个题我们发现都是跟梯形相关的,第一题是常规的梯形,根据面积的变化分析即可。而第二题水渠是一个立体的建筑,建筑中涵盖了梯形这一平面图形,想要分析暴雨后增加的水量,则需要根据水位增加的截面面积,结合水渠的长度进一步分析。
另外,近年来联考中几何问题考查的越来越多,越来越灵活,同学们一定要把知识点理解透彻了,做到简单几何问题迅速解决,复杂几何问题进行图形的分割转换,分解成多个部分进行分析。
下一篇:没有了

贴心微信客服


10w+
阅读量150w+
粉丝2w+
点赞数