2021-11-15 08:44:58 吉林公务员考试网 jl.huatu.com 文章来源:抚松华图
行测数资备考干货之利用鸡兔同笼巧解方程-抚松华图
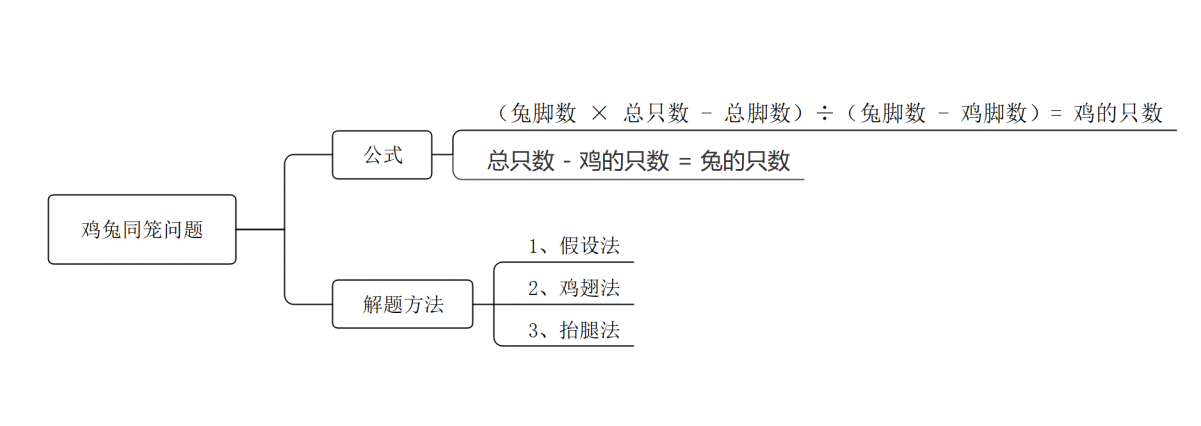
鸡兔同笼是中国古代的数学名题之一 ,早在 《 孙子算经 》 中就有了这样的叙述:今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何? 意思是有鸡和兔子在一个笼子里,能看到有35个头和94 条腿,问有鸡和兔子各几只。 这个问题本质上是一种二元方程,题设条件包括了不同数量的头和腿,那这种问题如何快速解决呢? 这里我们采用假设法。假设35个头全部都是兔子,那么应该有35×4=140条腿。但是现在实际只有94 条腿,假设比实际多了46 条腿。一只鸡变成一只兔子会多出2条腿,那么多出的46 条腿,应该是46 ÷ 2 = 23 只鸡在假设的时候变成了兔子,因此是有23 只鸡,而兔子数量就是35-23=12只。
由此我们对鸡兔同笼问题作出引申,当题目中出现两个不同的对象 ,而这两个不同的对象又同时拥有两种 不同特性时,我们就可以使用鸡兔同笼的思想来解决问题。如以下两道例题。
【真题1】 某赛事实行积分赛制,获胜积5分,打平积2分,失败扣1分。已知小辉在20场积分赛后积61分且有3场比赛打平,那么小辉的胜率为 ( ) :
A. 48% B. 55%
C. 60% D. 75%
【答案】C
【解析】 第一步,本题考查基础应用题, 可用鸡兔同笼思想解题。
第二步,由题意可得,获胜的场次和失败的场次总共有20-3=17场,得分为61-2×3=55分。 本题看似有三个主体,实则因为给出平场数,因此只剩胜场和负场两个不同的对象,即胜场和负场分别是“鸡”与“兔”。而胜场和负 场的场次数和可获得积分则是这两个对象共同拥有的特性,分别为鸡兔同笼问题中的“头”和“腿”。由此假设17 场全是胜场,求出此时积分为5×17 =85 , 比实际多得了85-55=30分 。而这个30 分的差距是由负场得到,因此用30 的积分差除以单次胜负场的积分差6,得到负场数量为5,再用总场数17-5 得到胜场数为12 。 即小辉的胜率为12÷20=60%。
因此,选择C选项。
【真题 2 】 小明负责将某农场的鸡蛋运送到小卖部。按照规定,每送到1枚完整无损的鸡蛋,可得运费0.1元;若鸡蛋有损,不仅得不到该鸡蛋的运费,每破损一枚鸡蛋还要赔偿0.4元。小明10月份共运送鸡蛋25000枚,获得运费2480元。那在运送的过程中,鸡蛋破损了 ( )
A.20枚 B.30枚
C.40枚 D.50枚
【解析】 第一步,本题考查基础应用题, 可用鸡兔同笼思想解题。
第二步,由题意可得,本题分为好鸡蛋和坏鸡蛋两个对象, 即鸡兔同笼问题中的“鸡“与”兔” 而这两个对象又有个数和运费两个不同的特性 ,即鸡兔同笼问题中的“头”与“腿”。先假设2 5000 枚鸡蛋都是好鸡蛋,那共应得到运费25000 × 0.4 = 2500 元,与实际的运费2 480元差距2500-2480 = 20 元。这20 元的差距由坏鸡蛋和好鸡蛋的差距得到。每个坏鸡蛋与好鸡蛋的运费差距为0 .4- (- 0.1 )= 0.5 元,因此坏鸡蛋数量为 枚。
因此,选择C选项。
【 小结 】
根据这两道题目我们发现,对于两个主体共同拥有两个特性的题目,我们可以利用鸡兔同笼的思想,通过假设法,不设未知数列方程快速解答问题。而解答的关键在于,准确区分材料中的不同主体与特性,确定可以采用鸡兔同笼的思想解决问题。
【 思维导图 】
想要了解更多公务员考试技巧,添加抚松华图微信号19969533559
以上就是【行测数资备考干货之利用鸡兔同笼巧解方程-抚松华图】的相关介绍,如果要了解更多热门资讯,欢迎关注吉林华图教育。

贴心微信客服
下一篇:没有了