国考行测之“十字交叉法”与“混合比值”的不解之缘

国考行测之“十字交叉法”与“混合比值”的不解之缘

　　国考行测之“十字交叉法”与“混合比值”的不解之缘

　　点击领取备考干货

　　说起十字交叉法，我们并不陌生，其具体操作挺简单，但对于方法背后的原理我们却往往是一知半解，对于运用的场景也是拿捏不准。今天我们一起来揭开其神秘面纱。

　　由小窥大——十字交叉法的本质

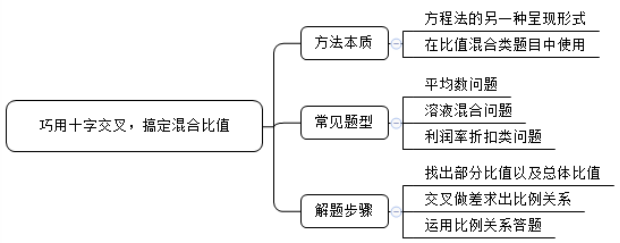
　　十字交叉法实际是方程法的另一种呈现形式，在比值混合类题目中使用十字交叉法往往能快速解题，达到事半功倍的效果。

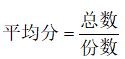
　　数量中常考查的平均数()是比值类题目，当涉及部分混合成整体时就可以归属于比值混合类了。我们以“平均分”为例，简单地理解下十字交叉背后的原理。

　　“已知在一次竞赛中，男选手的平均得分为80分，女选手的平均得分为65分，全部选手的平均得分为72分，能否求出男女选手人数之比为多少?”。在这个题目中，我们可以简化为要使男女得分混合之后稳定在72分，则要求男选手拉高的分数等于女选手拉低的分数。

　　从方程层面来说，设男女选手人数分别为x人，y人，每个男选手拉高8分(80-72=8)，每个女选手拉低7分(72-65=7)，则8x=7y，也就是x∶y=7∶8。

　　如何用十字交叉的图解形式快速清晰呈现呢?

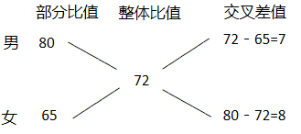
　　图示中把部分量的比值写成上下两列，整体量的比值写在交叉位置中央，最后交叉计算差值就可以。这里需要注意两点，一个是差值的计算中只关注差值绝对值，用大数减去小数就可以;另一个是通过十字交叉得到的差值的意义，即差值之比是比值中对应的分母之比，在平均分中也就是份数之比，即此题中的人数之比。这样，通过一个简单的图解形式，做一步简单的减法运算，就可以得到男女人数之比为7∶8。

　　由点及面——十字交叉法在比值混合题型中的运用

　　结合前文所说，十字交叉法适用的信号特征主要是以下三个：涉及部分与整体;给出部分比值、整体比值中的两个量或三个量;常用来解决两者之间的比例关系以及部分比值、整体比值的求解。

　　常见题型主要包括：

　　①平均数问题，平均数的交叉差值之比为人数之比。

　　②溶液混合问题，浓度的交叉差值之比为溶液质量之比。

　　③利润率折扣类混合问题， 利润率/折扣的交叉差值之比为总成本之比(当单件成本相同时，总成本之比等于销量之比)。

　　除此之外，行测中资料分析中的比重混合问题、增长率混合问题也可以用十字交叉法来解决。

　　牛刀小试——以真题窥实力

　　【例题】小张去机票代理处为单位团购机票10张，商务舱定价1200元/张，经济舱定价700元/张。由于买的数量较多，代理商就给予优惠，商务舱按定价的9折付钱，经济舱按定价的6折付钱，如果他付的钱比按定价少31%，那么小张一共买了经济舱票的票数是：

　　A. 7张 B. 6张

　　C. 9张 D. 8张

　　【答案】D

　　【解析】本题属于利润率折扣类混合问题，考虑采用十字交叉法解题。

　　第一步，找出部分比值以及总体比值。本题中比值形式体现为折扣，部分比值分别为9折(90%)、6折(60%)，整体比值为“比按定价少31%”，也就是69折(69%)。

　　第二步，十字交叉法求解比例关系(总成本之比)。如图所示。

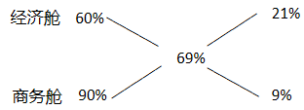
　　可得经济舱与商务舱的总成本之比为21%∶9%=7∶3。

　　第三步，设经济舱票数为x张，商务舱票数为y张，根据总成本的比例关系以及总票数，则有，可得x=8，即经济舱票数为8张。

　　因此，选择D选项。

　　以上就是巧用十字交叉法来快速解决比值混合类问题，你学会了么?

　

以上就是【国考行测之“十字交叉法”与“混合比值”的不解之缘】的相关介绍，如果要了解更多热门资讯，欢迎关注吉林华图教育。