2021-07-28 10:35:27 吉林公务员考试网 jl.huatu.com 文章来源:华图教育
关注【吉林华图】公众号获取更多考试资讯  点击关注
点击关注
2022国考行测数量关系:巧解不定方程-吉林大路华图
相信大家对方程都不陌生,我们从小学就开始接触方程,方程就是指含有未知量的等式。在行测数量关系题目中常常存在等量关系,我们可以通过列方程建立等量关系来解题。方程又分为两种类型,分别是定方程和不定方程。除了常见的定方程中的一元一次方程,二元一次方程组等,在国考数量关系中还会考查不定方程,那么什么是不定方程呢?

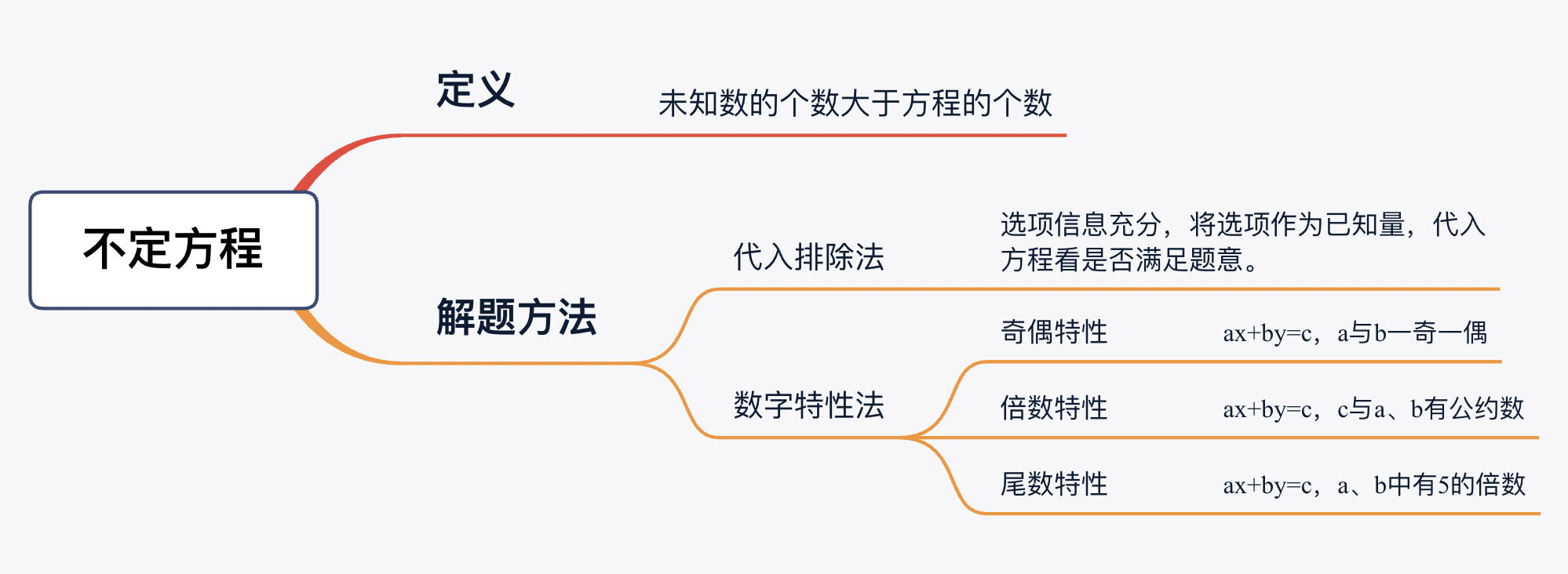
不定方程指未知数的个数大于方程的个数。比如:3x+4y=25,5x+8y=34……,在考试中遇到不定方程该如何快速求解呢?小编接下来就给大家介绍不定方程的解法。
代入排除法
选项信息充分,将选项作为已知量,代入方程看是否满足题意。
【例】3x+4y=25,求x,y各为多少?
x=2,y=5 B.x=4,y=3
C.x=5,y=3 D.x=3,y=4
华图点拨:选项信息充分,我们将选项依次代入。A选项,3×2+4×5=26,错误。B选项,3×4+4×3=24,错误。C选项,3×5+4×3=27,错误。D选项,3×3+4×4=25,正确。
数字特性法
不定方程:ax+by=c。
当a,b存在一奇一偶,可利用奇偶特性解不定方程。
【例】5x+4y=30,求x,y(均为正整数)各为多少?
华图点拨:利用奇偶特性,两个数和为偶数则两个数奇偶性相同,和30为偶数,所以5x和4y奇偶性相同,4y为偶数,5x也为偶数,故x为偶数:x=2,4,6……,又需满足5x+4y=30,综上x=2,y=5或x=6,y=0。
当c与a,b有公约数,可利用倍数特性解不定方程。
【例】3x+7y=49,x,y(均为正整数)各为多少?
华图点拨:利用倍数特性,7y为7的倍数,49为7的倍数,故3x一定为7的倍数,所以x为7的倍数,x=7,14……,又因为3x+7y=49,解得x=7,y=4或x=14,y=1。
当a,b中有5的倍数时,可利用尾数特性解不定方程。
【例】7x+10y=31,x,y(均为正整数)各为多少?
华图点拨:利用尾数特性,10y的尾数为0,31的尾数为1,故7x的尾数一定为1,又因7x+10y=21,7乘3的尾数为1,故x=3,y=1。
经过小编的讲解,大家有没有熟悉掌握不定方程如何解答呢?下面我们一起做一道真题检验一下吧!
C.5 D.6(2020四川)某人花400元购买了若干盒樱桃。已知甲、乙、丙三个品种的樱桃单价分别为28元/盒、32元/盒和33元/盒,问他最多购买了多少盒丙品种的樱桃?A.3 B.4
华图点拨:本题考查的是不定方程的问题。我们可以设分别购买了甲、乙、丙三个品种的樱桃x、y、z盒。根据题意可以列等式28x+32y+33z=400,观察可知28x、32y、400均为4的倍数,根据倍数特性,33z也必定是4的倍数,故z为4的倍数,观察选项,只有B选项符合题意。
经过小编的讲解,相信大家对于不定方程如何求解已经做到心中有数了,在以后数量关系的备考中,遇到不定方程的题型,大家一定要多多运用小编教大家的方法,这样才能熟能生巧,提高效率。跟上小编的步伐一起备考吧!
以上就是【2022国考行测数量关系:巧解不定方程-吉林大路华图】的相关介绍,如果要了解更多热门资讯,欢迎关注吉林华图教育。

贴心微信客服
上一篇:2022国考行测数量关系工程问题秒杀技巧-吉林大路华图
下一篇:没有了