行测知识点：函数最值题型巧解

行测知识点：函数最值题型巧解

　　结合近年来的行测题目分析，数量关系部分整体考情变化不大。经济利润问题几乎是每年的必考题型，其中包括基础公式问题、分段计费问题、费用统筹问题三类题型。而今天要分享的函数最值是费用统筹问题中常考的一类题型。因为此类题目技巧性比较强，且解题方法比较固定，只要多花一点时间稍加学习和练习，就能在考场上快速正确的做出来。

　　一、 题型识别

　　单价和销量此消彼长，问何时总价或总利润最高?

　　二、 解题思路

　　设提价/降价次数为 n。

　　算法：

　　(1)对称轴时取到最大值，即时有最大值。

　　(2)令总价或总利润为 0，解得n1、n2;当时，取得最值。

　　(3)和定积最大，通过提取公因数将未知数前的系数化为相反数，令前后两部分相等。

　　三、 真题讲解

　　【例1】将进货单价为90元的某商品按100元一个出售时，能卖出500个，已知这种商品如果每个涨价1元，其销量就会减少10个，为了获得最大利润，售价应定为：

　　A. 110元

　　B. 120元

　　C. 130元

　　D. 150元

　　正确答案： B

　　【解析】解法一：

　　第一步，本题考查经济利润问题，函数最值类。

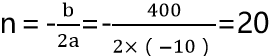
　　第二步，设涨价n元时，可得利润=(10+n)(500-10n)=-10n²+400n+5000。则，y取得最大值。

　　第三步，此时售价为100+20=120(元)。

　　因此，选择B选项。

　　解法二：

　　第一步，本题考查经济利润问题，函数最值类。

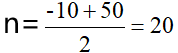
　　第二步，设涨价n元时，可得利润=(10+n)(500-10n),令10+n=0，500-10n=0，解得n1=-10，n2=50，，y取得最大值。

　　第三步，此时售价为100+20=120(元)。

　　因此，选择B选项。

　　解法三：

　　第一步，本题考查经济利润问题，函数最值类。。

　　第二步，设涨价n元时，可得利润y =(10+n)(500-10n)=10(10+n)(50-n)，令10+n=50-n，解得n=20。

　　第三步，此时售价为100+20=120(元)。

　　因此，选择B选项。

　　【例2】某企业设计了一款工艺品，每件的成本是70元，为了合理定价，投放市场进行试销。据市场调查，销售单价是120元时，每天的销售量是100件，而销售单价每降价1元，每天就可多售出5件，但要求销售单价不得低于成本。则销售单价为多少元时，每天的销售利润最大?

　　A. 100元

　　B. 102元

　　C. 105元

　　D. 108元

　　正确答案：C

　　【解析】解法一：

　　第一步，本题考查经济利润问题，函数最值类。

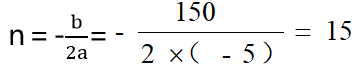
　　第二步，设降价了n元，则单件工艺品利润为(120-70-n)元，销量为(100+5n)件。总利润为(50-n)×(100+5n)=-5n2+150n+5000，取得最大值。

　　第三步，此时的售价为120-15=105(元)。

　　因此，选择C选项。

　　解法二：

　　第一步，本题考查经济利润问题，函数最值类。

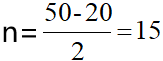
　　第二步，设降价了n元，则单件工艺品利润为(120-70-n)元，销量为(100+5n)件。总利润为(50-n)×(100+5n)，令50-n=0,100+5n=0,解得n1=50,n2=-20,。

　　第三步，此时的售价为120-15=105(元)。

　　因此，选择C选项。

　　解法三：

　　第一步，本题考查经济利润问题，函数最值类。

　　第二步，设降价了n元，则单件工艺品利润为(120-70-n)元，销量为(100+5n)件。总利润为(50-n)×(100+5n)=5×(50-n)×(20+n)，令50-n=20+n时取得最大值，此时n=15。

　　第三步，此时的售价为120-15=105(元)。

　　因此，选择C选项。

　　以上就是经济利润问题中函数最值的知识点、解题方法和真题讲解。函数最值整体难度中等，方法固定，解法一共有三种，在考场上建议使用的是第二种和第三种方法，因为此两种方法计算时间较短且正确率比较高。机会总是留给有准备的人。多掌握一种题型，就离上岸更近一步。

以上就是【行测知识点：函数最值题型巧解】的相关介绍，如果要了解更多热门资讯，欢迎关注吉林华图教育。