2024年国考行测高分技巧：最值问题何时了-数列构造知多少？

2024年国考行测高分技巧：最值问题何时了-数列构造知多少？

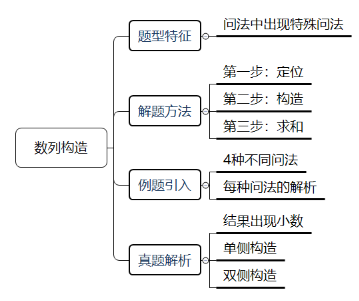
　　最值问题对于初学者来说比较难，对于一些题目不知如何下手。但是只要我们掌握相应的解题技巧，这类的题目也就迎刃而解。下面我们就最值问题中的一种常考题型-数列构造讲解一下。数列构造的题型特征是问法中出现“最多的最少、最多的最多、最少的最少、最少的最多、排名第几的最多或最少”。解题方法分为三步走：定位-构造-求和。具体识别题目和运用，我们先看一个例子：

　　有25个苹果，5个小朋友分，每人至少1个，每人分的个数各不相同

　　假设5个小朋友排成一排，从左至右分的个数依次减少。

　　①最多的人最多分几个?

　　第一步定位：第1个小朋友分的最多

　　第二步构造：因总数是一定的，要想最多的人分的最多，则其他小朋友要分的尽可能少，又因为各不相同，则从后面构造：第5个小朋友分1个、第4个小朋友分2个、第3个小朋友分3个、第2个小朋友分4个

　　第三步求和：X+4+3+2+1=25，求得X=15个。

　　②最多的人最少分几个?

　　最少X个 X-1 X-2 X-3 X-4

　　第一步定位：第1个小朋友分的最少

　　第二步构造：因总数是一定的，要想最多的人分的最少，则其他小朋友要分的尽可能多，又因为各不相同，则第2个小朋友最多分X-1个、第3个小朋友最多分X-2个、第4个小朋友最多分X-3个、第5个小朋友最多分X-4个

　　第三步求和：X+X-1+X-2+X-3+X-4=5X-10=25，求得X=7个

　　③最少的人最多分几个?

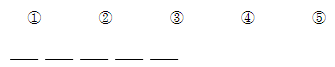
　　X+4 X+3 X+2 X+1 最多X个

　　第一步定位：第5个小朋友分的最多

　　第二步构造：因总数是一定的，要想最少的人分的最多，则其他小朋友要分的尽可能少，又因为各不相同，则第4个小朋友最少分X+1个、第3个小朋友最少分X+2个、第4个小朋友最少分X+3个、第5个小朋友最少分X+4个

　　第三步求和：X+X+1+X+2+X+3+X+4=5X+10=25，求得X=3个

　　④第二多的人最多分几个?

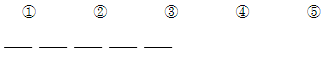
　　X+1 X 3 2 1

　　第一步定位：第2个小朋友分的最多

　　第二步构造：因总数是一定的，要想第二多的人分的最多，则其他小朋友要分的尽可能少，又因为各不相同，则第1个小朋友最少分X+1个、第5个小朋友最少分1个、第4个小朋友最少分2个、第5个小朋友最少分3个

　　第三步求和：X+1+X+3+2+1=2X+7=25，求得X=9个

　　经过上面四种不同的问法和解析，大家应该会对数列构造有一定的认识。接下来让我们畅游在真题的海洋中。

　　单侧构造：

　　【例1】现有21本故事书要分给5个人阅读，如果每个人得到的数量均不相同，那么得到故事书数量最多的人至少可以得到( )本。

　　A. 5 B. 7

　　C. 9 D. 11

　　【答案】B

　　【解析】

　　第一步，本题考查最值问题，属于数列构造。

　　第二步，在总数一定的条件下，要使得到故事书数量最多的人本数最少，那么其他人得到的要尽可能多。设得到故事书数量最多的人可以得到x本，且每个人得到的数量均不相同，则其余4人得到的故事书数量依次为(x-1)、(x-2)、(x-3)、(x-4)本。

　　第三步，根据题意可得x+(x-1)+(x-2)+(x-3)+(x-4)=21，解得x=6.2。所以最多的人至少可以得到7本。

　　因此，选择B选项。

　　大家可以发现此题最终解出的数值有小数，当出现这种情况时，我们应该问少取大，问多取小。也就是说当题目问法问的是最少的时候，当出现小数时，我们往上取整;当题目问法问的是最多的时候，当出现小数时，我们往下取整。

　　双侧构造：

　　【例2】从某物流园区开出6辆货车，这6辆货车的平均装货量为62吨，已知每辆货车载重量各不相同且均为整数，最重的装载了71吨，最轻的装载了54吨。问这6辆货车中装货第三重的卡车至少装载了多少吨?

　　A. 59 B. 60

　　C. 61 D. 62

　　【答案】B

　　【解析】

　　第一步，本题考查最值问题，属于数列构造。

　　第二步，总和一定，求某项最值，使用数列构造的方法。首先，根据题意将6辆货车的载重量从大到小排序则第一重的为71吨，最轻的为54吨，求第三重的卡车至少载重多少，则其余货车载重尽量多，设第三重的卡车至少载重x吨，那么构造排名第二至第五的载重依次为：70，x，x-1，x-2。可列方程：71+70+x+(x-1)+(x-2)+54=62×6，解得x=60。

　　因此，选择B选项。

　　通过这两个例子，同学们应该对数列构造类的最值问题有一定的了解，希望大家把上面的例题好好思考一下，做到融会贯通，此类题目就会举一反三。

以上就是【2024年国考行测高分技巧：最值问题何时了-数列构造知多少？】的相关内容，如果要了解更多国考行测高分技巧,最值问题何时了,数列构造知多少相关内容，欢迎关注吉林华图教育。