公务员考试行测数量关系空瓶换水的常见题型

公务员考试行测数量关系空瓶换水的常见题型

　　在近几年的行测考试中，数量关系部分的统筹问题考察频率有所提升，逐渐成为考试 “新宠”。面对这种灵活多变的题型，很多考生都选择了放弃。在此给大家分享一种统筹问题中常见模型——空瓶换水问题的解题方法，助力大家在考场上能快速拿分。

　　基本原理

　　我们通过下面这一道题目来探究一下这类题目的通用解法。

　　例1

　　3个空啤酒瓶可以免费换一瓶啤酒，现有32个啤酒空瓶，请问最多可以免费喝多少啤酒?

　　A.13 B.14 C.15 D.16

　　【答案】D。常规解析：很多同学拿到这类题目，往往就是一步一步地去换：

　　第一步：32个空瓶可以拿出30个空瓶来换10瓶啤酒，还剩2个空瓶;

　　第二步：把这10瓶啤酒喝掉可以得到10个空瓶，那么就一共有12个空瓶，再拿去换4瓶啤酒;

　　第三步：把这4瓶啤酒喝掉可以得到4个空瓶，拿出3个空瓶换1瓶啤酒，这时还剩下1个空瓶;

　　第四步：把这1瓶啤酒喝掉可以得到1个空瓶，一共就有了2个空瓶。2个空瓶看似不够换一瓶，但实则我们可以借1个空瓶过来，凑够3个空瓶，换得1瓶啤酒喝掉后再把借来的这1个瓶子还掉就可以了。

　　这样一共可以免费喝10+4+1+1=16瓶，故选择D选项。

　　但这个方法非常浪费时间，而且最后这个瓶子是需要借的，很多同学想不到这点。所以为大家带来一种更快解题的方法：

　　解析：根据题意3个空瓶=1瓶啤酒，我们可以把这1瓶啤酒看成1个空瓶加1份酒，得到3个空瓶=1个空瓶+1份酒，那么等式两边的1个空瓶可以消掉，变成2个空瓶=1份酒，也就是有2个空瓶就可以喝1份酒，那么32个空瓶就可以喝32÷2=16瓶酒，故选择D项。

　　【模型特征】：已知兑换规则及空瓶数，求最多能喝到的瓶数。

　　【基本公式】：假设n个空瓶可以换一瓶水，那么m个空瓶最多可以喝到m÷(n-1)瓶水。

　　灵活考法

　　为了让大家能够更好地掌握这类题型，我们再一起来了解一下它常见的变形。

　　例2

　　某啤酒开展“12个空瓶换1瓶啤酒”的大型促销活动，小张和他朋友在活动期间共喝了245瓶啤酒，那么他们至少需要买多少瓶啤酒?

　　A.223 B.224 C.225 D.226

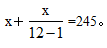
　　【答案】C。解析：根据题意小张和他朋友喝的245瓶啤酒包括了花钱买的和通过兑换得到这两部分。因此这道题本质上还是空瓶换水的思路：将一瓶啤酒看成1个空瓶+1份酒，所以根据兑换规则得到12空瓶=1空瓶+1份酒，也就是11空瓶=1份酒，设买了x瓶水，可得：解得想x≈224.6，因为x为正整数且最少为224.6，所以n向上取整为225，故选择C项。

　　通过这道题可以得到空瓶换水问题的变形总结：已知兑换规则及喝到的水数，求至少买多少瓶。这类题目只需要利用兑换规则列方程求解即可。值得注意的是当未知数解出来为非整数时，记得取整。

　　在行测考试中，大家如果遇到空瓶换水的问题，只需抓住空瓶换水的规则就可快速解题，希望今天分享能够为大家的备考起到一定的助力作用。

以上就是【公务员考试行测数量关系空瓶换水的常见题型】的相关内容，如果要了解更多公务员考试行测数量关系空瓶换水的常见题型相关内容，欢迎关注吉林华图教育。