2022-12-06 09:01:53 吉林公务员考试网 jl.huatu.com 文章来源:敦化华图
事业单位备考资料:改变思想解几何问题
数量关系的题目中常见题型里有几何问题,几何问题也经常会考到求图形的面积,但是在同学们实际做题过程中经常会使用到的方法只有基本公式这一种方法。可是,有一些题目使用基本公式进行求解过程中花费的时间较长,今天给大家推荐一种求面积的想法,帮助大家在解题时提高效率。
例1:已知正方形ABCD边长为6,正方形CEFG边长为4,求三角形BDF的面积为多少?
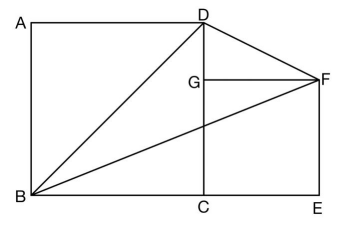
解析:此题是在求解三角形面积,不少同学会想到使用三角形的面积公式:底×高÷2进行计算。但是通过观察此三角形,底和高的长度都不方便计算,所以可以转变思路进行求解。我们可以想象将三角形BDF从完整的长方形中切割出来,首先可以补齐大的长方形即延长AD和EF交于H点。再用长方形ABEH的面积减去三角形ABD、三角形BEF和三角形DHF的面积,就可以得到三角形BDF的面积。其中长方形ABEH的长为两个正方形边长加和:6+4=10,宽为大正方形边长:6,可求得其面积为60;三角形ABD面积为正方形ABCD面积的一半:36÷2=18;三角形BEF面积=10×4÷2=20;三角形DFH面积=4×2÷2=4.所以所求三角形BDF的面积=60-18-20-4=18。
例2:现有一正方形花园ABCD其中E、F分别为BC和CD的中点,其中三角形AEF中种红色花且面积为36平方米,其余区域种植白色花,求白色花种植面积为?
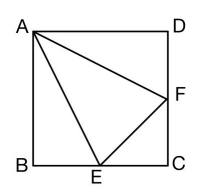
解析:题目所求为白色花种植面积即三角形ABE、三角形CEF、三角形ADF的面积之和,但是题目给出条件中并没有正方形的边长,所以直接使用三角形的面积公式进行求解并不简便。所以可以转变思路寻找三个三角形面积与正方形面积的关系。因为E为BC重点,所以三角形ABE的底BE为正方形边长的一半,三角形ABE面积=AB×BE÷2,正方形面积=AB×BC,所以可得三角形ABE面积为正方形ABCD的1/4;同理可得三角形ADF面积为正方形面积的1/4。此外因为F为CD中点,CF=CD÷2,三角形CEF面积=CE×CF÷2=BC÷2×CD÷2÷2,即三角形CEF面积为正方形ABCD面积的1/8。所以三角形ABE、三角形CEF、三角形ADF的面积之和为正方形ABCD面积的5/8。而整个正方形花园除白花外就是红花,所以三角形AEF面积为正方形ABCD面积的3/8。又因为正方形面积的3/8为36,所以正方形面积为96,白花面积为96×5/8=60平方米。
综上所述,我们在解决几何问题中求面积的题目时,除了直接使用面积公式进行求解,还可以采用割补或代换的思想解决问题,希望大家在之后做题过程中可以多多思考,同一道题目可以转变想法进行求解,经过练习,相信大家在之后做题中能更好地解决此类问题。
以上就是【事业单位备考资料:改变思想解几何问题】的相关介绍,如果要了解更多热门资讯,欢迎关注吉林华图教育。

贴心微信客服