2022-09-30 14:41:56 吉林公务员考试网 jl.huatu.com 文章来源:通化华图
排列组合之异素均分问题易错点剖析
数量关系是行测考试中难度颇高的一个板块,其主要考察应试者理解、把握事物间量化关系和解决数量关系问题的技能,主要涉及数字和数据关系的分析、推理、判断运算等,其中,排列组合的异素均分问题是很多同学都很难做正确的一类题目,但只要我们研究清楚其问题的本质,便可轻松做对此类题目。
一、从问法上识别“异素均分”问题
异素均分,就概念而言,就是把不同的元素进行平均分组
例如:m个不同的元素,平均分为n个组,一共有多少种情况?
二、“异素均分”问题破解思路
![]()
把m个不同的元素平均分成n组,接着我们采用分步的原理来计算,首先从m个元素当中取出a个元素,接着从剩下的元素当中再取出a个元素,一直重复下去,每次都取a个元素,等到全部元素取完便可终止,最后再分析这个过程中所包含的情况数。
1.异素均分分堆问题
例1
某中学有8个运动员,要平均分成2组,一共有几种分法?
A.25 B.70 C.35 D.90
![]()
【答案】C。解析:8个运动员平均分成2组,每组4人。首先从8个运动员中选出4个人,接着从剩下的4个人中选出4个人,因为整个过程是分步进行的,所以总的方法数等于各个步骤的方法数相乘,但其实这样做是存在问题的,我们可以把这8个人用abcdefgh这8个字母依次来表示,其中的一种情况可以是abcd为一组,那么剩下的efgh就自然成为另外一组了,当然也有可能是先挑出了efgh为一组,则abcd为一组,这两种分组方式前后对比会发现是同一种分组方式,都是abcd为一组,efgh为一组,所以算重复了2次,实际上的情况数为
通过这个题目我们可以看出,平均分成2组,算重复了2次,如果平均分成3组,会算重复几次呢?
例2
将红、橙、黄、绿、蓝、白6颗不同颜色的玻璃球,平均分成3堆,一共有几种情况?
A.15 B.45 C.60 D.90
【答案】A。解析:6颗不同颜色的玻璃球等同于6个不同的元素,平均分成3堆,每堆2颗玻璃球。首先,从6颗玻璃球中取出2颗;接着从剩下的4颗玻璃球中取2颗;最后从剩下的2颗中选出2颗,同样的我们还是选取其中的一种情况(红橙、黄绿、蓝白)来分析。
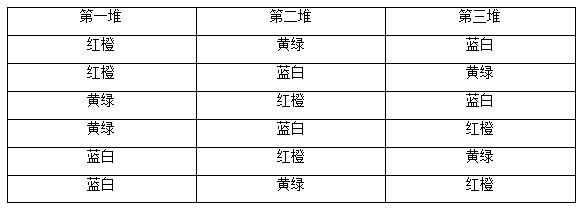
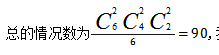
通过这个表格的简单罗列,我们便可以清楚地发现这6种情况都是同一种分堆情况,即红橙一堆,黄绿一堆,蓝白一堆,算重复了6次,我们可以进一步总结前一个题目平均分成两组,算重复了2次,本质上是算重复了本题平均分成3组,算重复了6次,所以可以得到异素均分问题平均分成n组,
2.异素均分分配问题
例题
某公司将旗下的6名歌手两两组成一个队,到三个不同的省会城市参加巡演,共有多少种不同的巡演情况?
A.15 B.45 C.60. D.90

【答案】D。解析:本题为异素均分问题,6名歌手两个人为一个队,即平均分成3队。根据前面所讲分成3队,因为3个队是去到3个不同的城市巡演,
相信大家通过上述题目,能对异素均分问题有所了解,建议大家在备考期间多多练习,真正掌握这类问题,也希望能对大家的备考有所帮助。
更多备考资料欢迎电话咨询:0435-3500222
以上就是【排列组合之异素均分问题易错点剖析】的相关介绍,如果要了解更多热门资讯,欢迎关注吉林华图教育。

贴心微信客服