2022-08-31 16:32:00 吉林公务员考试网 jl.huatu.com 文章来源:净月华图
2023年国考数资备考技巧之容斥问题的公式
无论是在国考省考中,还是在各种事业单位的考试中,容斥问题都是常考的题型。但是考生对这种题型却非常的头疼,无从下手。其实只要大家掌握了容斥问题的公式,这类题目也就迎刃而解了。
![]()
容斥问题主要分为两集合和三集合这两种类型。首先两集合容斥原理的公式为:。对于此种题型,只需要在题目中将对应量找到代入公式中即可。我们通过一个例题练习一下。
【例1】某班有38名学生,一次数学测验共有两道题,答对第一题的有26人,答对第二题的有24人,两题都答对的有17人,则两题都答错的人数是:
A. 3 B. 5
C. 6 D. 7
【解析】第一步,本题考查容斥问题,属于二集合容斥类。
第二步,设两题都答错的人数为x,根据二集合容斥公式,可得38-x=26+24-17,解得x=5。因此,选择B选项。

接下来再学习一下三集合容斥原理的公式。

标准型:

非标准型:
![]()
可以看出这两个公式比较相似,那么我们怎样区分哪一个题目应该用哪个公式呢?就是看题目当中给出的条件的个数,如果给出了这样的三个条件,那么就用三集合标准型的公式,如果给出了“只满足两个条件的个数”这样的一个条件,那么就用三集合非标准型的公式。接下来我们通过题目练习一下吧!
【例2】针对100名旅游爱好者进行调查发现,28人喜欢泰山,30人喜欢华山,42人喜欢黄山,8人既喜欢黄山又喜欢华山,10人既喜欢泰山又喜欢黄山,5人既喜欢华山又喜欢泰山,3人喜欢这三个景点,则不喜欢这三个景点中任何一个的有多少人?
A.20 B.18
C.17 D.15
E.14 F.13
G.12 H.10
【解析】第一步,本题考查容斥原理,属于三集合容斥类,用公式法解题。

第二步,因为题目中给出“8人既喜欢黄山又喜欢华山,10人既喜欢泰山又喜欢黄山,5人既喜欢华山又喜欢泰山”这种条件给出了三个,因此用三集合标准型公式计算即可。设不喜欢任何一个景点的有x人,根据公式,得出100-x=28+30+42-8-10-5+3,解得x=20。因此,选择A选项。
【例3】如图所示:A、B、C分别是面积为60、170、150的三张不同形状的卡片,它们部分重叠放在一起盖在桌面上,总共盖住的面积为280,且A与B、B与C、C与A重叠部分的面积分别是22、60、35。问阴影部分的面积是多少?
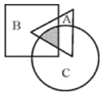
A. 15 B. 16
C. 17 D. 18
【解析】第一步,本题考查容斥问题,属于三集合容斥类,用公式法解题。
第二步,设阴影部分面积为x,由总共盖住的面积为280,根据三集合标准公式可得:280-0=60+170+150-22-60-35+x,解得x=17(也可利用尾数法,计算尾数为7)。因此,选择C选项。
【例4】某班参加学科竞赛人数40人,其中参加数学竞赛的有22人,参加物理竞赛的有27人,参加化学竞赛的有25人,只参加两科竞赛的有24人,参加三科竞赛的有多少人?
A.2 B.3
C.5 D.7
【解析】第一步,本题考查容斥问题,属于三集合容斥类,用公式法解题。第二步,题干“只参加两科竞赛的有24人”这种条件只给出了一个,所以用三集合非标准型的公式。设参加三科竞赛的有x人,根据公式可列方程:40-0=22+27+25-24-2x,解得x=5。因此,选择C选项。
以上就是【2023年国考数资备考技巧之容斥问题的公式】的相关介绍,如果要了解更多热门资讯,欢迎关注吉林华图教育。

贴心微信客服
上一篇:2023国考行测资料分析之巧用特殊分数解决增长量计算
下一篇:没有了