公务员考试行测排列组合的四种常用方法

公务员考试行测排列组合的四种常用方法

　　行测考试之中，数量关系是大多数考生的痛点也是难点，特别是排列组合问题更是让大家望而却步。但是对于这类题目，只要大家掌握一定的解题方法，问题就可以迎刃而解了。下面重点给大家介绍排列组合问题中常用的一些方法，并能够辨识每种方法的应用环境。

　　方法介绍

　　优限法：有特殊元素或特殊位置的排列问题，通常是先安排特殊元素或特殊位置，即优先处理特殊元素(或位置)法，简称优限法。

　　捆绑法：当出现元素相邻(或挨在一起等表述)时，先将相邻元素进行捆绑看作一个整体，再与其他元素进行排列，并且需要考虑被捆绑元素的顺序。

　　插空法：当出现元素不相邻(或不能挨在一起等表述)时，先将其他元素排好，再将所指定的不相邻的元素插入到他们的间隙或两端位置。

　　间接法：在解决至多至少等问题时，正向求解比较复杂，我们可以反向求解，用总的方法数减去对立面(反面)的方法数即可得到我们的所求。

　　方法应用

　　例题

　　由数字 1、2、3、4、5 组成无重复数字的五位数，

　　(1)数字 1 必须在首位或末尾的五位数有________个。

　　(2)两个偶数必须相邻的五位数有________个。

　　(3)两个偶数互不相邻的五位数有________个。

　　(4)至少有一个偶数在前两个位置的五位数有________个。

　　【答案】48;48;72;84。解析：

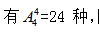
　　(1)数字1有特殊要求，则先排数字1，有2种;再排其余数字，有因此所求为 2×24=48 个。

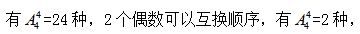
　　(2)2个偶数必须相邻，则将2个偶数捆绑在一起看成1个数，与剩余的3 个数进行排列，故所求为 24×2=48个。

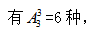
　　(3)先排3个奇数，再从奇数形成的4个空位里选2个将剩余 2 个偶数放入，因此所求为6×12=72个。

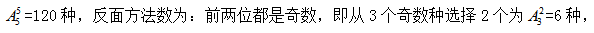
　　(4)两个偶数中至少有一个在前两个的位置，即包含了有一个或者是两个均在前两个位置中，情况较多，不太容易求解，故考虑用间接求解，即总的方法数-反面方法数=所求方法数。总的方法数为：故为6×6=36种，所求为：120-36=84种。

　　例题展示

　　例1

　　有8人要求在某学术报告会上做报告，其中甲、乙要被安排在前三个，丙要在最后一个，丁不在前三个，则共有多少种可能的报告顺序?

　　A.553 B.576 C.283 D.266

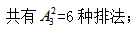
　　【答案】B。解析：甲、乙要在前三，可以优先安排他们的顺序，其次，丙在最后一个，共有1种排法;最后丁不在前三个，同时也不可能是最后一个，所以只有中间四个位置可以选择，因此所求为：6×4×24=576种顺序，故选择B项。

　　例2

　　为加强机关文化建设，某市直机关在系统内举办演讲比赛，3个部门分别派出3、2、4名选手参加比赛，要求每个部门的参赛选手比赛顺序必须相连，问不同参赛顺序的种数在以下哪个范围之内?

　　A.小于1000 B.1000~5000

　　C.5001~20000 D.大于20000

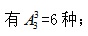
　　【答案】B。解析：每个部门的参赛选手比赛顺序必须相连，即将每个部门的人进行捆绑，看作一个整体，即公3个部门;首先考虑三个部门的出场顺序，其次考虑每个部门选手的出场顺序，则不同参赛顺序的种数为 6×6×2×24=72×24，计算结果显然大于1000，小于5000，故选择B项。

　　以上便是介绍的关于排列组合问题的一些常见方法以及求解思路，值得注意的是，在做这类问题的时候，需要我们理解每种方法的应用场景，而很多题目往往要同时用到多种方法，这就更需要我们熟练运用这些方法，所以同学们还要加强练习。

以上就是【公务员考试行测排列组合的四种常用方法】的相关介绍，如果要了解更多热门资讯，欢迎关注吉林华图教育。