2022-07-15 09:44:09 吉林公务员考试网 jl.huatu.com 文章来源:吉林华图
2023年公务员考试行测数量关系备考:打破“经济问题”屏障
我们一生中每时每刻都在与钱打交道,所以谈起经济,相信大家并不陌生。但陌生的是在公务员考试当中,出题人把一个生活化的例子用专业术语抽象表达出来时大家便会一头雾水。就此本文给大家浅谈一下经济问题中一种看似高端,实则可以秒杀的问题:统筹优化类题型找最值问题(最值优化类题型)。
首先,欲学此功先打好基本功,而谈起经济问题怎么都离不开利润、成本、进价、收入、售价、定价、销量、打折、利润率等字眼。大家再细品其中有些量的关系其实也是一致的,比如售价本质也就是你收到的钱即收入,进价其实也就是成本。当我们结合我们生活中常见的买卖交易,好像这些量我们就能用专业的数学语言来表示出来:

1.利润=售价(收入)-进价(成本)
2.总利润=单利润×销量=(售价-进价)×销量
3.售价=定价×折扣
4.利润率=利润/成本(数量关系)
接下来,当大家已经对经济问题有了一个初步感觉之后,紧接着就要给大家上题了:
【例1】某商品的进货单价为80元,销售单价为100元,每天可售出120件,已知销售单价每降低1元,每天可多售出20件。若要实现该商品的销售利润最大化,则销售单价应降低的金额是:
A.5元
B.6元
C.7元
D.8元
【答案】:C
【解析】:本题所求为销售单价降低多少使总利润最大,可设销售单价降低x元,则每天可多售出20x件,根据公式:总利润=(售价-进价)×销量可得:总利润=(100-x-80)×(120+20x)=(20-x)×(120+20x)。此题为一元二次函数求最值,方法多样化:
法一:代入排除法求最大值:A选项总利润=(20-5)×(120+20×5)=3300,同理B选项总利润=(20-6)×(120+20×6)=3360,C选项总利润=(20-7)×(120+20×7)=3380,D选项总利润=(20-8)×(120+20×8)=3360,因此C选项最大。
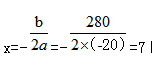
法二:利用二次函数性质求最值,总利润=-20false+280x+2400,根据二次函数性质,时,函数取最大值即总利润最大;
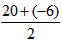
法三:利用二次函数图像零点求最值,总利润=(20-x)×(120+20x),当(20-x)×(120+20x)=0时,x1=20,x2=-6,此时两零点的中点即x==7时为最大值,所以x=7时总利润最大。
法四:利用均值不等式和定积最大的性质求最值,总利润=(20-x)×(120+20x)=(20-x)×20(6+x),这时候(20-x)+(6+x)=26为定值,当且仅当他们相等即(20-x)=(6+x)时乘积最大,所以x=7时总利润最大;
一题四法供大家选择,在真正步入考场的时候可适当选择自己喜欢并运用熟练解法解题,当然图兔给大家建议还是以三、四法为主,对于二次函数熟练度高的小伙伴以第三法为主即可快速秒杀题目。
接下来,给大家一个例题小试一下牛刀:
【例2】某企业设计了一款工艺品,每件的成本是70元,为了合理定价,投放市场进行试销。据市场调查,销售单价是120元时,每天的销售量是100件,而销售单价每降价1元,每天就可多售出5件,但要求销售单价不得低于成本。则销售单价为多少元时,每天的销售利润最大?
A.100元
B.102元
C.105元
D.108元
【答案】:C
![]()
【解析】:本题同样需求解销售总利润最大,设每降低x元,每天就可以多卖5x件衣服,根据题意可列方程销售总利润=(120-x-70)×(100+5x),令(120-x-70)×(100+5x)=0可得:x1=50,x2=-20,当x==15时取最大值,即当120降低15元为105元时,每天销售利润最大,因此,选择C选项。
以上就是【2023年公务员考试行测数量关系备考:打破“经济问题”屏障】的相关介绍,如果要了解更多热门资讯,欢迎关注吉林华图教育。

贴心微信客服
下一篇:没有了