公务员考试行测数量关系：正向求解心好累?逆向思维来解围

公务员考试行测数量关系：正向求解心好累?逆向思维来解围

　　在行测数量关系的学习过程中，考生总会遇到一部分题目从正面入手去计算或者利用方程的思想解题都很复杂，最终往往既浪费了时间又没有选出结果，而对于这种看似复杂的题目，只要掌握了一定的技巧和思维，也可以很简单。下面要介绍的是数量关系当中一种重要的解题思维：逆向思维。

　　所谓逆向思维，即：如果一道题从正面求解所涉及的情况比较复杂，计算起来比较麻烦的话，那么我们就可以从其相对的一面进行考虑，或者以最终状态作为突破口进行反推计算，以此来简化问题的一种解题思维。在计算问题、排列组合问题以及概率问题等题型中，逆向思维都有其“用武之地”。

　　例1

　　30个人围坐在一起轮流表演节目。他们按顺序从1到3依次不重复地报数，数到3的人出来表演节目，并且表演过的人不再参加报数，那么仅剩一个人没表演过节目的时候，共报数多少人次?

　　A.77 B.57 C.117 D.87

　　【解析】此题若正向分析，则需梳理整个报数过程才可枚举出报数的人次数，情况较为复杂，因此可以考虑利用逆向思维，从最终状态入手。由于最后仅剩一人没有表演过节目，因此共有30-1=29人表演过节目，又因为每报数3人次即有1人表演节目，所以共报数29×3=87人次。故本题选D。

　　小结：对于正向分析情况复杂的计算问题，可以结合题干条件，以最终状态作为突破口进行反推计算。

　　例2

　　单位组织拔河比赛，每支参赛队伍由3名男职工和3名女职工组成，假设比赛时要求3名男职工不能全连在一起，则每支队伍有多少种不同站位方式?

　　A.432 B.504 C.576 D.720

　　【解析】此题要求3名男职工不能全连在一起，若正向分析，满足该要求的情况可分为两大类：①3名男职工互不相邻;②其中2位男职工相邻，且与第三位男职工不相邻。而第二类情况中还需进一步分析哪两位男职工相邻，分类较为复杂，计算方法数时容易出现遗漏或重复，这时我们可以尝试利用逆向思维解题。

　　“3名男职工不全连在一起”的对立面是“3名男职工全连在一起”，利用捆绑法可得“3名男职工全连在一起”对应的方法数为因此，所求“3名男职工不全连在一起”的方法数为720-144=576种。故本题选C。

　　小结：对于正向分析情况复杂的排列组合问题，可以考虑利用逆向思维，先计算题干要求的对立面方法数以及总方法数，用“总方法数-对立面方法数”即为所求。

　　例3

　　桌子中有编号为1-10的10个小球，每次从中抽出1个记下后放回，如是重复3次，则3次记下的小球编号乘积是5的倍数的概率是多少?

　　A.43.2% B.48.8% C.51.2% D.56.8%

　　【解析】此题若从正向分析，满足“3次记下的小球编号乘积是5的倍数”的情况有以下三大类：①仅有一次抽到编号为5或10的球②有且仅有两次抽到编号为5或10的球③三次抽到的都是编号为5或10的球。而前两类情况中还需进一步分析是哪一次以及哪两次抽到编号为5或10的球，情况仍然复杂。我们还是利用逆向思维求解这道题，即：乘积是5的倍数的概率=1-乘积不是5的倍数的概率。

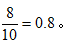
　　由于是有放回抽取，所以每次所取小球编号总的样本数为10个，取出的小球编号不是5的倍数的样本有8个，那么每次所取小球编号不是5的倍数的概率为要满足3次的编号乘积不是5的倍数，就要让每一次所取球的编号都不是5的倍数，3次取球的过程相互独立，所以3次的编号乘积不是5的倍数的概率=0.8×0.8×0.8=0.512，所求为1-0.512=0.488，即48.8%。故本题选B。

　　小结：对于正向分析情况复杂的概率问题，同样可以考虑利用逆向思维，先分析并计算对立事件发生的概率，再用“1-对立事件发生的概率”即为所求。

　　相信通过以上三道例题，各位考生已经对如何应用逆向思维解题有了一定的了解，逆向思维求解的关键在于，要分析清楚与题干要求相对立的情况是什么。想要将逆向思维真正融会贯通，还需各位考生在备考期间勤加练习，多多思考总结。

以上就是【公务员考试行测数量关系：正向求解心好累?逆向思维来解围】的相关介绍，如果要了解更多热门资讯，欢迎关注吉林华图教育。