2022-06-21 09:23:42 吉林公务员考试网 jl.huatu.com 文章来源:吉林华图
2022年松原市公务员技巧行测数量关系:超越平均速度感受数字之美
什么是平均速度
平均速度常常用来粗略地描述一段时间内的运动情况。
通常在题目所给出的一段时间内,几段路的速度不相同,要求全程的平均速度。
平均速度为什么容易错
在求解平均速度时,许多小伙伴习惯性地将一段时间内内全程的平均速度,误以为是速度加和的平均,导致最终计算结果有误。
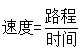
需要注意的是,速度并非独立的计量的量,是通过“”公式,经过计算得到的,会受到路程与时间的影响。因此在求平均速度时,不能用速度加和后再做除法这样简单地来进行计算。
例如:大雄和静香以1m/s的速度,从学校到1000米外的空地。到达空地时恰好碰到胖虎唱歌,所以立刻以7m/s跑了2米钻进水泥管里。
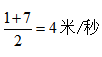
即使我们根据生活常识来判断整体的运动情况,也能够感受到,大雄在这段时间内,并不会以这样的平均速度————如同贴了“急行符”一样地运动的。
那么,平均速度到底如何来进行求解呢?
平均速度怎么做
虽然出题形式多样,但万变不离其宗。我们最有力的方法,即是根据形成问题中的核心概念公式解题。
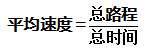
重点在于找到速度、路程、时间之间的等量关系,进而求解出问题的答案即可。下面我们一起通过例题来熟悉应用。
例1
![]()
四名运动员参加4×100米接力,他们100米速度分别为不考虑其他影响因素,他们跑400米全程的平均速度为:
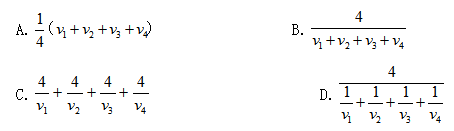
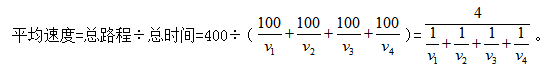
【答案】D。解析:
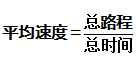
思考:应对平均速度问题,可用核心公式求解。
例2
![]()
汽车在平直的公路上运动,它先以速度v行驶了的路程,接着以30km/h的速度驶完余下的路程。若全程平均速度是40km/h,则v是多少?
A.60km/h B.70km/h C.80km/h D.90km/h
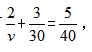
【答案】C。解析:设总路程为5,则汽车以速度v行驶的路程为2,以30km/h行驶的路程为3。根据题意有解得v=80km/h。
思考:求解平均速度,可通过题干找到等量关系,通过时间相同从而建立方程。
例3
一辆汽车第一天行驶了5个小时,第二天行驶了600千米,第三天比第一天少行驶200千米,三天共行驶18小时,已知第一天的平均速度与三天全程的平均速度相同,则三天共行驶了多少千米?
A.800 B.900 C.1000 D.1100
【答案】B。解析:设三天全程的平均速度为v千米/时,则第一天行驶距离为5v千米,第三天行驶距离为(5v-200)千米,根据题意有5v+600+5v-200=18v,解得v=50,则三天共行驶了18×50=900千米。
思考:通过第一天与三天全程的平均速度相同,可根据路程相等建立等量关系。
平均速度的特殊情况
![]()
当所给出的两段运动的路程相等时,则这两段路程的平均速度可用:“”求解。其中 公式里的v1、v2,分别为这两段路程上的速度。
很明显,如果一道题目的描述符合平均速度公式的应用环境时,可套用公式快速求解。下面我们通过例题来进一步熟悉这个知识。
例4
甲去北京出差,去时坐飞机,返回时坐高铁,若飞机的速度比高铁快3倍,且往返平均速度为480千米/小时,问甲乘坐的飞机速度为多少千米/小时?
A.720 B.768 C.960 D.1200
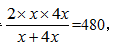
【答案】D。解析:飞机比高铁快3倍,则飞机的速度是高铁的3+1=4倍。设高铁的速度为x千米/小时,则飞机的速度为4x千米/小时,利用平均速度公式可得x=300,则飞机速度为1200千米/小时,选择D。
思考:当题干所给出的两段运动路程相等,则可巧用平均速度公式,套用公式快速解题。从而达到节省时间的目的。
例5
张红和李健同时从班级出发沿同一条路线去食堂,若张红用一半的时间以速度x行走,另一半时间以速度y行走;李健在前一半路程以速度x行走,后一半路程以速度y行走(x≠y),则下列说法正确的是:
A.张红和李健同时到达食堂 B.李健先到达食堂
C.张红先到达食堂 D.两人谁先到达食堂不能确定
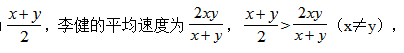
【答案】C。解析:从班级到食堂的路程一定,由平均速度公式可知,张红的平均速度为张红先到达食堂,选择C。
思考:当题目中出现了两段运动的时间/路程相等时,注意区分两者异同。
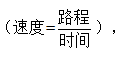
1、当两段运动的时间相同,则可用基础公式因此其平均速度不能套用平均速度公式,而应为:
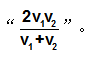
2、当两段运动的路程相等时,则可用平均速度公式
掌握问题本质,抓住核心概念,练好解题本领——超越他人做题的“平均速度”,来感受数学之美吧。
以上就是【2022年松原市公务员技巧行测数量关系:超越平均速度感受数字之美】的相关介绍,如果要了解更多热门资讯,欢迎关注吉林华图教育。

贴心微信客服