2022-06-10 10:02:35 吉林公务员考试网 jl.huatu.com 文章来源:净月华图
23国考数量关系中工程问题考查重难点
工程问题是国考行测数量关系模块中常考知识点,也是数量关系中在考场上相对于其他题型容易拿分的。考查比较常规的是给定时间型、给定效率型,赋值结合方程一起求解,还有一类较难的题型是统筹类工程问题。
赋值类
1.给定时间型:赋工程总量,一般让其为所给几个时间的最小公倍数,找效率求解。
【例1】(2017年国考)工厂有5条效率不同的生产线。某个生产项目如果任选3条生产线一起加工,最快需要6天整,最慢需要12天整;5条生产线一起加工,则需要5天整。问如果所有生产线的产能都扩大一倍,任选2条生产线一起加工最多需要多少天完成?
A.11
B.13
C.15
D.30
【答案】C
【解析】本题为给定时间型工程问题,赋值法。加入五条生产线的效率分别为,
![]()
【解析】本题为给定时间型工程问题,赋值法。加入五条生产线的效率分别为,,那么效率最大的三条效率和为,所需时间为6天整,5条一起生产效率和为,所需时间为5天整,所以赋工程总量为30,那么效率为6,那么效率为1。产能扩大一倍,那么的效率变为原来的2倍。所以选择的两条最慢的一起加工所需时间为(天)。因此选C。
,那么效率最大的三条效率和为
![]()
【解析】本题为给定时间型工程问题,赋值法。加入五条生产线的效率分别为,,那么效率最大的三条效率和为,所需时间为6天整,5条一起生产效率和为,所需时间为5天整,所以赋工程总量为30,那么效率为6,那么效率为1。产能扩大一倍,那么的效率变为原来的2倍。所以选择的两条最慢的一起加工所需时间为(天)。因此选C。
,所需时间为6天整,5条一起生产效率和为
![]()
【解析】本题为给定时间型工程问题,赋值法。加入五条生产线的效率分别为,,那么效率最大的三条效率和为,所需时间为6天整,5条一起生产效率和为,所需时间为5天整,所以赋工程总量为30,那么效率为6,那么效率为1。产能扩大一倍,那么的效率变为原来的2倍。所以选择的两条最慢的一起加工所需时间为(天)。因此选C。
,所需时间为5天整,所以赋工程总量为30,那么
![]()
【解析】本题为给定时间型工程问题,赋值法。加入五条生产线的效率分别为,,那么效率最大的三条效率和为,所需时间为6天整,5条一起生产效率和为,所需时间为5天整,所以赋工程总量为30,那么效率为6,那么效率为1。产能扩大一倍,那么的效率变为原来的2倍。所以选择的两条最慢的一起加工所需时间为(天)。因此选C。
效率为6,那么
![]()
【解析】本题为给定时间型工程问题,赋值法。加入五条生产线的效率分别为,,那么效率最大的三条效率和为,所需时间为6天整,5条一起生产效率和为,所需时间为5天整,所以赋工程总量为30,那么效率为6,那么效率为1。产能扩大一倍,那么的效率变为原来的2倍。所以选择的两条最慢的一起加工所需时间为(天)。因此选C。
效率为1。产能扩大一倍,那么
![]()
【解析】本题为给定时间型工程问题,赋值法。加入五条生产线的效率分别为,,那么效率最大的三条效率和为,所需时间为6天整,5条一起生产效率和为,所需时间为5天整,所以赋工程总量为30,那么效率为6,那么效率为1。产能扩大一倍,那么的效率变为原来的2倍。所以选择的两条最慢的一起加工所需时间为(天)。因此选C。
的效率变为原来的2倍。所以选择的两条最慢的一起加工所需时间为
![]()
【解析】本题为给定时间型工程问题,赋值法。加入五条生产线的效率分别为,,那么效率最大的三条效率和为,所需时间为6天整,5条一起生产效率和为,所需时间为5天整,所以赋工程总量为30,那么效率为6,那么效率为1。产能扩大一倍,那么的效率变为原来的2倍。所以选择的两条最慢的一起加工所需时间为(天)。因此选C。
(天)。因此选C。
2012年联考真题也出现过和本题非常类似的题目,给三个时间,但是我们在赋值工程总量的时候只需考虑两个时间即可,并非给几个时间就要用几个时间。本题亦可根据过程量快速推测答案,产能扩大一倍,工程总量保持不变,那么效率和时间是反比关系,时间要减半。
2.给定效率型:可以是直接给定效率比也可以是通过给定等量关系间接给出效率之间比值关系。一般直接对给定的效率之比进行赋值,按最简比例赋值,然后找工程量求解。
【例2】(2018年国考) 工程队接到一项工程,投入80台挖掘机。如连续施工30天,每天工作10小时,正好按期完成。但施工过程中遭遇大暴雨,有10天时间无法施工。工期还剩8天时,工程队增派70台挖掘机并加班施工。问工程队若想按期完成,平均每天需多工作多少个小时?
A. 2.5
B. 3
C. 1.5
D. 2
【答案】D
【解析】赋值每台挖掘机的效率均为1,根据题意把找等量关系列方程求解即可。设平均每天多
![]()
【解析】赋值每台挖掘机的效率均为1,根据题意把找等量关系列方程求解即可。设平均每天多工作小时,那么,解得。因此选D。
工作小时,那么,解得
![]()
【解析】赋值每台挖掘机的效率均为1,根据题意把找等量关系列方程求解即可。设平均每天多工作小时,那么,解得。因此选D。
。因此选D。
此类题目还经常变形表述为每个工人效率相同的工程队,那么赋最简比例,让每个人的效率都为1,再去求解。
【例3】(2019年国考)有甲、乙、丙三个工作组,已知乙组2天的工作量与甲、丙共同工作1天的工作量相同。A工程如由甲、乙组共同工作3天,再由乙、丙组共同工作7天,正好完成。如果三组共同完成,需要整7天。B工程如丙组单独完成正好需要10天,问如由甲、乙组共同完成,需要多少天?
A.不到6天
B.6天多
C.7天多
D.超过8天
【答案】C
【解析】间接给效率之比的工程问题。根据题意
![]()
【解析】间接给效率之比的工程问题。根据题意,可知,所以赋甲、乙的效率分别为3、4,又因为,所以丙的效率为5。那么B的工程总量为,所以甲、乙合作所需时间为。因此选C。
,可知
![]()
【解析】间接给效率之比的工程问题。根据题意,可知,所以赋甲、乙的效率分别为3、4,又因为,所以丙的效率为5。那么B的工程总量为,所以甲、乙合作所需时间为。因此选C。
,所以赋甲、乙的效率分别为3、4,又因为
![]()
【解析】间接给效率之比的工程问题。根据题意,可知,所以赋甲、乙的效率分别为3、4,又因为,所以丙的效率为5。那么B的工程总量为,所以甲、乙合作所需时间为。因此选C。
,所以丙的效率为5。那么B的工程总量为
![]()
【解析】间接给效率之比的工程问题。根据题意,可知,所以赋甲、乙的效率分别为3、4,又因为,所以丙的效率为5。那么B的工程总量为,所以甲、乙合作所需时间为。因此选C。
,所以甲、乙合作所需时间为。因此选C。
统筹类工程问题:原则让效率高的尽可能多的做其擅长的工作,从而达到尽可能快的完成所有的任务。
绝对效率:一般出现两个工程队,要负责两项工程,两个工程队做这两项工程的效率分别一大一小,那么直接看绝对效率。
【例4】(2014国考)甲、乙两个工程队共同完成A和B两个项目。已知甲队单独完成A项目需13天,单独完成B项目需7天;乙队单独完成A项目需11天,单独完成B项目需9天。如果两队合作用最短的时间完成两个项目,则最后一天两队需要共同工作多长时间就可以完成任务?

【答案】D
【解析】本题考查统筹类工程问题,看绝对效率。甲每天做A、B的
![]()
【解析】本题考查统筹类工程问题,看绝对效率。甲每天做A、B的,乙每天做A、B的,二者均有一项效率高于对方,所以尽可能多的让甲做B工程,让乙做A工程,那么甲7天即可把B工程做完,此时再去帮乙一起做A工程,还需要(天)。那么最后一天两个队需共同工作的时间为天。因此选D。
,乙每天做A、B的
![]()
【解析】本题考查统筹类工程问题,看绝对效率。甲每天做A、B的,乙每天做A、B的,二者均有一项效率高于对方,所以尽可能多的让甲做B工程,让乙做A工程,那么甲7天即可把B工程做完,此时再去帮乙一起做A工程,还需要(天)。那么最后一天两个队需共同工作的时间为天。因此选D。
,二者均有一项效率高于对方,所以尽可能多的让甲做B工程,让乙做A工程,那么甲7天即可把B工程做完,此时再去帮乙一起做A工程,还需要
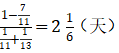
【解析】本题考查统筹类工程问题,看绝对效率。甲每天做A、B的,乙每天做A、B的,二者均有一项效率高于对方,所以尽可能多的让甲做B工程,让乙做A工程,那么甲7天即可把B工程做完,此时再去帮乙一起做A工程,还需要(天)。那么最后一天两个队需共同工作的时间为天。因此选D。
(天)。那么最后一天两个队需共同工作的时间为
![]()
【解析】本题考查统筹类工程问题,看绝对效率。甲每天做A、B的,乙每天做A、B的,二者均有一项效率高于对方,所以尽可能多的让甲做B工程,让乙做A工程,那么甲7天即可把B工程做完,此时再去帮乙一起做A工程,还需要(天)。那么最后一天两个队需共同工作的时间为天。因此选D。
天。因此选D。
2.相对效率:两个工程队、两项工程,某个工程队做两项工程效率均高,则看相对效率。
【例5】(2020年国考)甲、乙两条生产线生产A和B两种产品。其中甲生产线生产A、B产品的效率分别是乙生产线的2倍和3倍。现有2种产品各X件的生产任务,企业安排甲和乙生产线合作尽快完成任务,最终甲总共生产了1.5X件产品。问乙在单位时间内生产A的件数是生产B件数的多少倍?
![]()
【答案】C
【解析】本题考查统筹类工程问题,看相对效率。设甲生产A和B两种产品的效率分别为,乙生产A和B两种产品的效率分别为,甲生产两种产品效率均高于乙,但生产相同量的B产品,甲、乙所用的时间分别能生产A产品2份、3份。所以让乙尽可能多的生产A,根据二者合作所以两条生产线工作时间相同列方程,
![]()
【解析】本题考查统筹类工程问题,看相对效率。设甲生产A和B两种产品的效率分别为,乙生产A和B两种产品的效率分别为,甲生产两种产品效率均高于乙,但生产相同量的B产品,甲、乙所用的时间分别能生产A产品2份、3份。所以让乙尽可能多的生产A,根据二者合作所以两条生产线工作时间相同列方程,。因此选C。
。因此选C。
条件综合型:给的具体数值较多,结合方程法等求解。
【例6】(2020年浙江)甲、乙两企业合作完成某订单需要x天。如果甲企业产能增加50%而乙企业不变,可提前2天完成;如果乙企业产能增加300%而甲企业不变,可提前4天完成。问x的值是:
A.6
B.8
C.10
D.12
【答案】B
【解析】方程法,结合选项代入排除。根据题意列方程:设甲、乙的效率分别为,则
![]()
【解析】方程法,结合选项代入排除。根据题意列方程:设甲、乙的效率分别为,则,方程直接求解不易,结合选项代入A选项,那么,不符合题意,排除;代入A选项8,连等号两边均符合。因此选B。
,方程直接求解不易,结合选项代入A选项,那么,不符合题意,排除;代入A选项8,连等号两边均符合。因此选B。
此外,工程问题在近几年其他省份的考试中也出现了结合周期、时间等问题一起考查,考生要多加练习,这样在考场上才能游刃有余解决工程问题。更多相关考试信息请及时关注华图教育官网!

以上就是【23国考数量关系中工程问题考查重难点】的相关介绍,如果要了解更多热门资讯,欢迎关注吉林华图教育。

贴心微信客服
上一篇:23国考成语也有感情