知识点：工程问题之效率制约题型解析

知识点：工程问题之效率制约题型解析

　　行测各模块中，数量关系大概是令大多数考生最头疼的一个了，很多考生在考场上选择直接放弃，但数量关系其实是保证我们能否进面的一个关键，考试中可以选择做一些简单的题目，今天所说的工程问题中的效率制约型类的题目考试中出现难度一般不大，可以在平时的时候下功夫掌握之后，考场上就可以快速做出来。

　　一、 题型识别

　　题干中有给出不同主体的效率的比例关系或倍数关系

　　二、 解题思路

　　方法：赋值法

　　解题步骤：①根据比例关系赋值效率;

　　②计算工作总量;

　　③根据题意求解。

　　三、 真题讲解

　　【例1】有甲、乙、丙三个工作组，已知乙组2天的工作量与甲、丙共同工作1天的工作量相同。A工程如由甲、乙组共同工作3天，再由乙、丙组共同工作7天，正好完成。如果三组共同完成，需要整7天。B工程如丙组单独完成正好需要10天，问如由甲、乙组共同完成，需要多少天?

　　A. 不到6天

　　B.6天多

　　C. 7天多

　　D. 超过8天

　　正确答案： C

　　【解析】第一步，本题考查工程问题，属于效率制约型题目，用赋值法解题。

　　第二步，设三者工作效率分别为甲、乙、丙，根据题意则有2乙=甲+丙，3(甲+乙)+7(乙+丙)=7(甲+乙+丙)，可得3乙=4甲，赋值甲=3，则乙=4，解得丙=5。

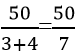
　　第三步，B工程总量=10丙=10×5=50，则甲乙合作需要天，即7天多。

　　因此，选择C选项。

　　【例2】某单位甲、乙、丙三人负责整理一项档案，他们工作5天完成了1/4，之后甲和乙因其他工作被调离，两天后才返回，期间丙继续整理档案。已知甲、乙、丙三人的工作效率之比为4∶3∶2，则完成这项工作共需要花费( )天

　　A. 20

　　B. 21

　　C. 22

　　D. 23

　　正确答案：C

　　【解析】第一步，本题考查工程问题，属于效率制约型题目，用赋值法解题。

　　第二步，赋值甲的效率为4，乙的效率为3，丙的效率为2。工作总量=4×5×(4+3+2)=180，其中有2天是丙单独干，工作量为2×2=4，剩余的工作量由甲乙丙合作干需要：，即20天。那么一共需要20+2=22天。

　　因此，选择C选项。

　　【例3】一场大雪过后，某单位需安排员工清扫包干区的道路积雪。清扫时必须3人一组，其中2人铲雪，1人扫雪。如果安排10人铲雪，3.5小时才能完成。假设每组工作效率相同，若要在100分钟内完成，则需安排的员工人数最少是：

　　A. 21

　　B. 24

　　C. 30

　　D. 33

　　正确答案：D

　　【解析】第一步，本题考查工程问题，属于效率制约型题目，用赋值法解题。

　　第二步,赋值每组每小时的工作效率为1，10人铲雪共有5组，则工作总量为5×3.5=17.5，100分钟=小时，则至少需要17.5÷=10.5(组)，即11组。

　　第三步，所以需安排的员工数为11×3=33(人)。

　　因此，选择D选项。

　　以上就是工程问题中的效率制约型问题的一些情况，这类型题目有的时候会直接给定效率的比值，例如：甲乙效率之比是2：3，有的时候会间接给出效率的比值，例如：甲3天的工作量等于乙4天的工作量，有的时候更是需要推导出效率的比值，解这类题目关键是要能识别出题型，按比例给效率赋值，然后计算工作总量，根据题意求解。

以上就是【知识点：工程问题之效率制约题型解析】的相关介绍，如果要了解更多热门资讯，欢迎关注吉林华图教育。