2022-05-05 13:33:00 教师招聘考试网 jl.huatu.com 文章来源:华图教育
2022中小学教师招聘备考之常见的函数模型求解的题型总结
函数部分最为教师招聘考试中非常重要的一个部分,主要会围绕函数导数应用相关,函数图像与性质,函数模型及应用等。今天主要围绕函数的模型及应用的部分跟大家分享一下常见考题类型,主要包括以下几种:(1)用图像去刻画变化规律,这种类型主要考察的是选择题;(2)已知函数解析式,结合函数解析式去解决实际情况,这种类型主要考察选择题或者解答题;(3)考生自主构造函数模型,如一次函数,二次函数,指数函数,分段函数等,这种类型考察解答题。
一、知识回顾
1.几类函数模型

2.三种函数模型的性质
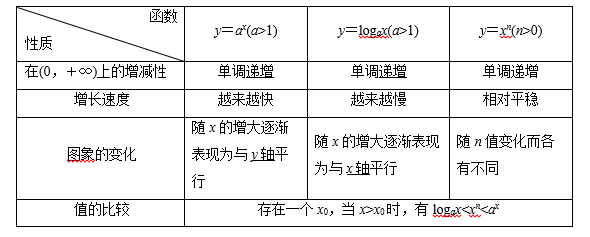
二、常见题型总结
类型一:用函数图象刻画变化过程
1.【2015年 安徽 中学】如图,正方形ABCD的边长为4厘米,动点P、Q同时从点A出发,沿正方形的边匀速运动,点P沿A-B-C方向移动,速度为1厘米/秒,点Q沿A-D-C-B方向移动,速度为2厘米/秒,两点相遇时停止移动。设△APQ的面积为y(平方厘米),移动时间为t(秒),则以下图象能正确反映y与t之间的函数关系的是()


类型二:已知函数模型的实际问题 1.某商场从生产厂家以每件20元的价格购进一批商品,若该商品零售价定为p元,销售量为Q件,则销售量Q(单位:件)与零售价p(单位:元)有如下关系:Q=8300-170p-p2,则最大毛利润为(毛利润=销售收入-进货支出)()
A.30元B.60元 C.28 000元D.23 000元
【答案】D
【解析】设毛利润为L(p)元,则由题意知 L(p)=pQ-20Q=Q(p-20)=(8300-170p-p2)(p-20)=-p3-150p2+11 700p-166000, 所以L′(p)=-3p2-300p+11 700. 令L′(p)=0,解得p=30或p=-130(舍去). 当p∈(0,30)时,L′(p)>0,当p∈(30,+∞)时,L′(p)<0,故L(p)在p=30时取得极大值,即最大值,且最大值为L(30)=23000. 知识拓展: 求解所给函数模型解决实际问题的关注点 (1)认清所给函数模型,弄清哪些量为待定系数. (2)根据已知利用待定系数法,确定模型中的待定系数. (3)利用该模型求解实际问题.
类型三:构建函数模型的实际问题
1.【2017年 安徽 小学】如图,在直角梯形ABCD中,AB//CD, ,且AB=8,AD=3,CD=4,动点P、Q分别以点B和点A为起点同时出发,点P沿B—>A,以每秒1个单位速度运动,终点为点A;点Q沿A—>D—>C—>B,以每秒1.5个单位速度运动,终点为B,设 的面积为y,运动时间为x秒。
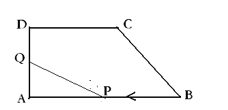
(Ⅰ)求y关于x的函数解析式 ;(Ⅱ)画出函数 的函数图象。

当 时 2.某城市为了加强公民的节气和用气意识,按以下规定收取每月煤气费:所用煤气如果不超过50立方米,按每立方米0.8元收费;如果超过50立方米,超过部分按每立方米1.2元收费。设小丽家每月用气量为 立方米,应交煤气费为 元。
(1)试写出 与 之间的表达式;
(2)若小丽家4月份的煤气费为88元,那么她家4月份所用煤气量为多少立方米?
(3)已知小丽家6月份的煤气费平均每立方米0.95元,那么6月份小丽家用了多少立方米的煤气?

三、总结提升
解函数应用题的一般步骤
第一步:(审题)弄清题意,分清条件和结论,理顺数量关系;
第二步:(建模)将文字语言转化成数学语言,用数学知识建立相应的数学模型;
第三步:(解模)求解数学模型,得到数学结论;
第四步:(还原)将用数学方法得到的结论还原为实际问题的意义;
第五步:(反思)对于数学模型得到的数学结果,必须验证这个数学结果对实际问题的合理性.

贴心微信客服