2022-03-28 13:57:41 吉林公务员考试网 jl.huatu.com 文章来源:华图教育
最多(少)的最少(多)的有多少——数列构造问题__梅河口华图
针对这些有固定套路的题,我们只需要掌握好对应的方法,遇到对应的题目,直接套用就可以了,例如:容斥问题、工程问题,最不利构造问题以及数列构造问题。下面就介绍一下关于数列构造问题的固定解题方法。
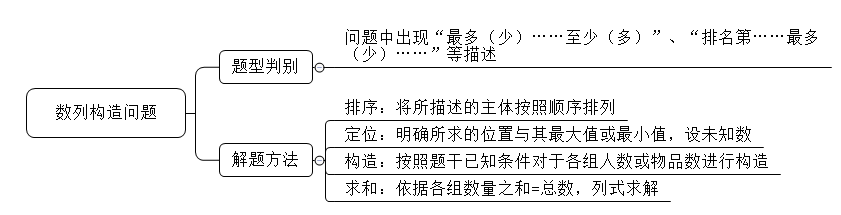
一、题型特点:题干是要求将人数或物品按照一定原则进行分组或分配,问题中出现“最多(少)……至少(多)”、“排名第……最多(少)……”等描述。
二、解题方法:排序-定位-构造-求和
排序:将所描述的主体按照顺序排列,确定最大值与最小值的位置。
定位:明确所求的位置,设未知数。
构造:按照题干已知条件对于各组人数或物品数进行构造。
求和:依据各组数量之和=总数,列式求解。
方法运用:
【示例】五位学生参加某次考试后平均分为90分,每个人的分都为整数且均不相同,问得分最低的学生最多得多少分?
排序:将五位同学按照分数从高到低排序。
定位:题目问的是的分最低的,设第五名得分为x。
构造:要使第五名得分最多,总分数为90×5=450是固定值,则其他人需要尽可能的少,第四名最少为x+1,第三名x+2,以此类推。
| 第一名 | 第二名 | 第三名 | 第四名 | 第五名 |
| x+4 | x+3 | x+2 | x+1 | x |
求和:总分数为450,则x+4+x+3+x+2+x+1+x=450,解得x=88,即得分最低的学生最多得88分。
三、真题感知
【例】某街道服务中心的80名职工通过相互投票选出6名年度优秀职工,每人都只投一票,最终A、B、C、D、E、F这6人当选。已知A票数最多,共获得20张选票;B、C两人的票数相同,并列第2;D、E两人票数也相同,并列第3;F获得10张选票,排在第4。那么B、C获得的选票最多为()张。
A.11B.12
C.13D.14
【答案】D
【解析】第一步,本题考查最值问题中的数列构造问题。
第二步,根据前述的解题方法,排序-定位-构造-求和,依题意先排序、定位列出表格如下:
要使B、C选票最多其他人需要尽可能的少,又D、E票数相同且要比F多,故,D、E最少取11。
第三步,总票数为80票,求和,20+x+x+11+11+10=80,解得x=14,即D、F最多得14票。
因此,选择D选项。
通过前述的示例和真题,相信大家应该掌握了解决数列构造问题的方法。方法的难点在于构造的过程,要仔细的分析清楚题干的要求,若求最多,其他的量就尽可能的少;求最少,其他量就需要尽可能的多。这类题需要充分结合题干的要求及条件,通过排序-定位-构造-求和这种方法求出对应的答案。
以上就是【最多(少)的最少(多)的有多少——数列构造问题__梅河口华图】的相关介绍,如果要了解更多热门资讯,欢迎关注吉林华图教育。

贴心微信客服