2022-03-26 11:35:08 吉林公务员考试网 jl.huatu.com 文章来源:伊通华图
2022年公务员考试行测数量关系:解直角三角形的灵魂方法_伊通华图
数量关系是行测备考中比较头疼的部分,但其实只要掌握好方法和技巧,很多题目解起来,游刃有余。今天就带领大家一起探究一下常见勾股数在解直角三角形中的妙用。
回顾旧知
1.勾股定理
直角三角形的两条直角边的平方和等于斜边的平方
2.常见勾股数
(3、4、5)、(6、8、10)、(5、12、13)
注:在常见勾股数的基础上扩大或缩小相同的倍数而得到的三条边,依旧满足勾股定理,进而可以推测出直角三角形中所需要求的那条边的值。
历年试题
例1
一个无盖长方体饮料盒如下图所示,其底面为正方形,高为23厘米。若插入一根足够细的不可弯折的吸管与底部接触,已知插入饮料盒内的吸管长度最大为27厘米,则饮料盒底面边长为多是厘米
![]()

![]()
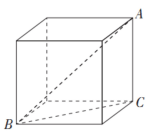
【答案】C。解析:由题目可知,如图所示,插入饮料盒内的吸管长度最大时是长方体的体对角线AB,与长方体的高AC、底面正方形的对角线BC,组成了一个直角三角形ABC。根据勾股的定理,可得正方形对角线因为正方形的边长与对角线的比为所以正方形边长为10厘米,根据选项可知,本题选择C项。
例2
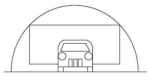
一个半圆形拱门的宽和高分别为8米和4米,一辆货车拉着宽4.8米、每层高20厘米的泡沫板通过该拱门。如果车斗底部与地面的垂直距离为1.1米,问如果要通过拱门,每次最多可以装载几层泡沫板?
A.9 B.10 C.11 D.12
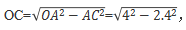
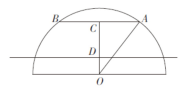
【答案】B。解析:当泡沫板的宽正好和拱门接触时,泡沫板的高度和最大,装载泡沫板的数量最多。如图所示,OD表示车斗底部与地面的距离,AB为泡沫板的宽。根据题意可知AB=4.8米,OA=4米,AC=2.4米,OD=1.1米。根据勾股定理,可知观察这个根式,很明显不好求解,此时我们就可以根据“在常见勾股数的基础上扩大或缩小相同的倍数而得到的三边,依旧满足勾股定理”将再结合常见勾股数(6、8、10)从而推出则泡沫板与车斗底部之间的最大距离为OC-OD=3.2-1.1=2.1米,又因为一层泡沫板高20厘米即0.2米,则能装的层数为因为层数必须为整数且不能再高了,所以取10层,根据选项可知,本题选择B项。
相信大家通过上述两道题目,能够发现勾股定理在帮助我们求解直角三角形时,除了可以直接代勾股定理求得某一条边的长度,也可以根据在“常见勾股数的基础上扩大或缩小相同的倍数而得到的三边,依旧满足勾股定理”,进而推测出直角三角形中所需要求的那条边的值。
以上就是【2022年公务员考试行测数量关系:解直角三角形的灵魂方法_伊通华图】的相关介绍,如果要了解更多热门资讯,欢迎关注吉林华图教育。

贴心微信客服