2023年国考行测备考之排列与组合解题技巧 _乾安华图

2023年国考行测备考之排列与组合解题技巧 _乾安华图

　　一.前言

　　在公务员国考行测的排列组合备考中，排列与组合模块几乎是历年的必考题，这些题目对于文科同学来说，比较晦涩难懂，不太容易拿到理想的分数，甚至很多同学对排列组合类的题目都有畏难情绪，这块知识需要我们在理解的基础上掌握相关的解题技巧，并且需要通过大量的做题，然后勤于总结才能做到心中有数。

　　二.历年考情

年份	2021	2020	2019	2018	2017
题量	1	2	1	1	1
比重	6.7%	13.3%	6.7%	6.7%	6.7%

　　注：以上是国家公务员考试省部级的历年考情。

　　三.基础知识

　　3.1排列与组合的区别

　　例1:从36位同学中选取2人参加竞赛，问共有多少种不同的选法?

　　例2：甲、乙、丙三个人到旅店住店，旅店里只有三个房间，恰好每个房间住一个人，问一共有多少种不同的住法。

　　我们发现从36人中选取2人，结果与选取的顺序无关，则为组合，记为C，满足的情况数为，三个房间按照三人排序的不同入住，结果也不同，那么这就是说结果与选取的顺序有关，则为排列，记为A，满足的情况数为，在此，我们做一下总结，排列与顺序有关，而组合与顺序无关。

　　3.2加法和乘法原理

　　例3：从A地到B地，可以乘坐高铁或飞机或大巴，则从A地到B地共有多少种不同的交通方式?

　　例4：制造一件零件需E、F共2道工序。完成E有3种方法，完成F有4种方法，则完成此零件共有几种制造方法?

　　在这里我们通过2道例题来说明加法和乘法两个原理，例3中我们无论乘坐高铁或飞机或大巴均可独立完成从A地到B地的事件，因此我们把从A到B分成了三类，每一类均可独立完成，总的不同的交通方式等于各类的满足情况数之和;例4中我们发现完成这个零件需要2道工序，每道工序均不能独立完成该事件，则这种情况我们称为分步，总的情况数等于每一步情况数相乘。

　　3.3基本公式的计算

　　四.方法与技巧

　　排列组合类的题，我们除了需要掌握相关的概念，能够区分出排列与组合的区别以及掌握排列组合的基本公式外，我们还需要掌握一些解题的方法和技巧，只有这样才能应对灵活多变的考题，做到知识点了然于胸。下面对常见的方法和技巧进行讲解。

　　4.1捆绑法

　　例5：ABCDE共5人排成一行，要求AB两人必须相邻，则共有多少种排列方式?

　　我们发现这是一道排列的题目，与顺序有关，题目要求AB相邻，这样我们可以把AB捆绑在一起看成一个元素，则将总的四个元素进行排列，然后AB的内部需要重排，即,整个过程属于分步，则总的排列方式等于。针对题目中出现相邻要求时，优先考虑捆绑法。

　　4.2插空法

　　例6：ABCDE共5人排成一行，要求AB两人不相邻，则共有多少种排列方式?

　　首先判断该题属于排列，与顺序有关，那么要求AB不相邻，这时候我们可以优先将CDE三人进行重排，即然后CDE形成了4个空，从这四个空中选出2个分别放入AB即可实现AB不相邻的要求，即,那么总的排列方式：。针对元素要求不相邻的题目，我们优先安排没有要求的元素，然后将要求不相邻的元素进行插空即可。

　　4.3隔板法

　　例7：把8个相同的苹果分给4个人，要求每人至少分得一个苹果，则共有多少种的分配方法?

　　题目出现了相同元素，并且出现了至少分一个的字眼的分配问题的时候，我们考虑是隔板法，这里直接将公式给出：将n个相同元素分给m个人，要求每人至少分得1个元素，则总的分配方式为，因此该题的分配方式为。

　　4.4环形排列

　　例8：3个小朋友围着一个圆桌吃饭，问共有多少种不同的安排方法?

　　本题是环形排列问题，与顺序有关，我们知道如果三个人直线排列，则共有种排列方式，那么环形排列有什么不同吗?我们可以看下图，我们发现图中的三种排列方式在环形中其实是一种排列方式，因此，将n个不同元素进行直线型排列的情况数是其环形排列情况数的n倍，即n个不同元素进行环形排列的总的排列数为：，因此三人圆桌吃饭不同情况排列数为。

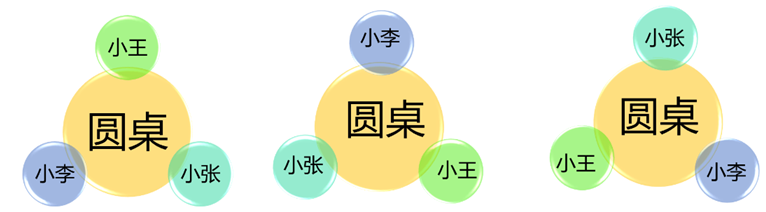
　　图1

　　五.小结

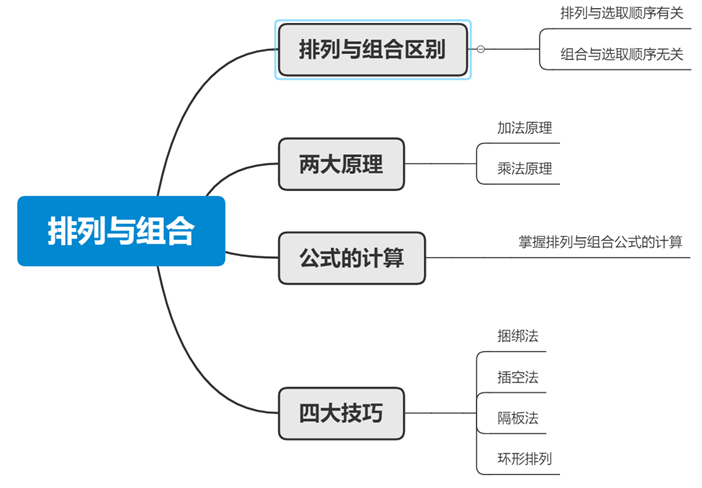
　　以上就是排列组合模块的探讨，希望通过以上的学习，同学们掌握排列与组合的区别，加法和乘法原理以及四种常用的方法和技巧，同学们也可以登录华图的官方网站和各地华图分院对不懂的问题及时与我们交流，在公务员备考的路上，华图与您一起风雨同舟。下图是本节的思维导图，供大家参考。

以上就是【2023年国考行测备考之排列与组合解题技巧 _乾安华图】的相关介绍，如果要了解更多热门资讯，欢迎关注吉林华图教育。