2022-03-05 16:42:11 吉林公务员考试网 jl.huatu.com 文章来源:通榆华图
公务员行测技巧:牛吃草问题的三种具体情况
牛吃草问题其实严格意义上来说应该叫做牛吃草模型,我们用一种通俗易懂的比喻将一些涉及到原始固定量受到两个因素的影响的基础应用题转化为追及问题。试想一下,我们可以把草地上所有的草拔出来,将其排列在一条直线上,我们近似可以看成一条路,牛在“路”的一端开始吃草,而草为了不被吃光以生长的状态逃离牛。这样就变成了追及问题。
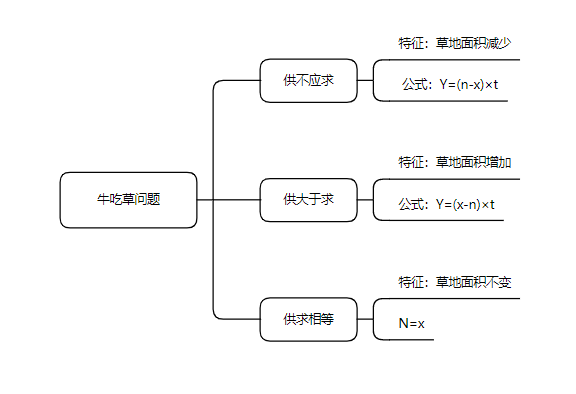
牛吃草问题一共可分为三类:供不应求、供大于求和供求相等,下面我们来详细说一下这三类题型该如何解答。
供不应求。
牧场上有一片匀速生长的草地,放N头牛去吃草且每头牛每天吃的草量相同。牛吃草使草量减少,草自身生长使草量增加,(前提:牛吃草的速度大于草自身生长的速度),这种情况称之为供不应求。假设T天牛把草吃完,同时假设这片草场原有量为y份,每头牛每天吃1份草,这片草场的草每天的生长速度为x份。则原有草量=(牛每天吃掉的量-草每天生长的量)×天数,整理可得:y=(N-x)×T。
【例1】某疫苗接种点市民正在有序排队等候接种。假设之后每小时新增前来接种疫苗的市民人数相同,且每个接种台的效率相同,经测算:若开8个接种台,6小时后不再有人排队;若开12个接种台,3小时后不再有人排队。如果每小时新增的市民人数比假设的多25%,那么为保证2小时后不再有人排队,需开接种台的数量至少为:
A.14个B.15个
C.16个D.17个
【解题思路】
根据牛吃草公式y=(N-x)T,y代表原有草量,即原有排队的市民数;N代表牛的头数,即所开接种台数量;x为草生长的速度,即每小时新增市民数;T代表时间。代入数据,y=(8-x)×6,y=(12-x)×3,解得x=4,y=24,每小时新增市民人数增加25%,则x变为4×(1+25%)=5,设至少需开N个接种台能保证2小时不再有人排队,代入公式得:24=(N-5)×2,解得N=17。选D。
供大于求。
牧场上有一片匀速生长的草地,放N头牛去吃草且每头牛每天吃的草量相同。牛吃草使草量减少,草自身生长使草量增加,(前提:牛吃草的速度小于草自身生长的速度),这种情况称之为供大于求。假设T天之后,草地的面积增加了y,每头牛每天吃1份草,这片草场的草每天的生长速度为x份。则草地增加的面积=(草每天生长的量-牛每天吃掉的量)×天数,整理可得:y=(x-N)×T。
【例2】假设一片牧场的青草一直都是“匀速”自然生长的,该牧场3月初放养有1000只羊,30天后青草的总量变为3月初的90%,此时牧场又一次性增加了300只羊。12天后青草的总量变为3月初的80%,如果要让青草在接下来4个月内(每月按30天计算)回到3月初的总量,则这4个月间该牧场至多放牧()只羊。
A.800B.750
C.700D.600
【解题思路】
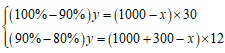
设牧场原有草量为y,草长的速度为x。列方程组:,解得x=800,y=60000。
设至多放牧N只羊,根据回到3月初的总量列方程:(100%-80%)y=(x-N)×120,即(100%-80%)×60000=(800-N)×120,解得n=700。
因此,选择C选项。
三.供求相等。
这种情况比较简单,只需把握住一个等量关系即N=x即可,在这里就不再赘述了。
相信通过这篇文章,同学们对于牛吃草问题应该有了一个较为清晰的认知,接下来只需要有针对性的进行刷题训练,就一定可以熟练掌握。
以上就是【公务员行测技巧:牛吃草问题的三种具体情况】的相关介绍,如果要了解更多热门资讯,欢迎关注吉林华图教育。

贴心微信客服
下一篇:没有了