2022年省考行测数量之《几何最值理论之平面图形》

2022年省考行测数量之《几何最值理论之平面图形》

　　行测数量关系模块包含的题型很多，其中几何问题可以说是每年省考必考的一种题型。学习几何问题首先要熟悉一些基本图形的面积或者体积公式，例如圆形的面积、圆柱的体积和球体的体积公式等;还要掌握一些几何特性，例如三角形不等式性质、相似三角形和几何最值理论等。今天介绍一下几何最值理论在平面图形中的应用，在具体讲解例题之前，大家要了解平面图形中的两条最值理论：

　　(1)平面图形中，若周长一定，越接近于圆，面积越大;

　　(2)平面图形中，若面积一定，越接近于圆，周长越小。

　　【例1】某健身馆准备将一块周长为100米的长方形区域划为瑜伽场地，将一块周长为160米的长方形区域划为游泳场馆。若瑜伽场地和游泳场馆均是满足周长条件下的最大面积，问两块场地面积之差为多少平方米?

　　A.625

　　B.845

　　C.975

　　D.1150

　　【答案】C

　　【解析】第一步，本题考查几何问题，用几何最值理论解题。

　　第二步，题干要求“瑜伽场地和游泳场馆均是满足周长条件下的最大面积”，根据几何最值理论：平面图形中，若周长一定，越接近于圆，面积越大。但平面图形如果是四边形，则越接近于正方形面积越大，所以周长为100米和160米的两个四边形，当其为正方形时面积最大。瑜伽场地的边长为100÷4=25米，面积为625平方米;游泳场馆场地的边长为160÷4=40米，面积为1600平方米。

　　第三步，两块场地面积之差为1600-625=975平方米。

　　因此，选择C选项。

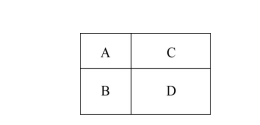
　　【例2】村民陶某承包一长方形地块，他将地分割成如图所示的A、B、C、D四个地块，其中A、B、C的周长分别是20米、24米、28米，D的最大面积是多少平方米?

　　A.42

　　B.49

　　C.64

　　D.81

　　【答案】C

　　【解析】第一步，本题考查几何问题，用方程法解题。

　　第二步，如图所示，设长方形A的宽为a，长为b，则a+b=10。长方形B的宽为c，则b+c=12。长方形C的长为d，则a+d=14，所以c+d=(a+d)+(b+c)-(a+b)=16，长方形D的周长为32。

　　第三步，周长一定，越接近正方形面积越大，故D为正方形时面积最大，边长为32÷4=8，面积为64。

　　因此，选择C选项。

　　【例3】某地市区有一个长方形广场，其面积为1600平方米。由此可知，这个广场的周长至少有?

　　A.160米

　　B.200米

　　C.240米

　　D.320米

　　【答案】A

　　【解析】第一步，本题考查几何问题。

　　第二步，根据几何特性，长方形面积一定，越接近于正方形时周长越小，则这个广场可直接为正方形，边长为40米，周长为4×40=160米。

　　因此，选择A选项。

　　以上三个例题就是几何最值理论在平面图形中的应用，如果掌握的牢靠，可以迅速地找到解题的技巧，省略了用图形公式解题的过程，避免了复杂的计算。希望感兴趣的同学可以研究研究，也希望今天通过我的讲解，对同学们的备考过程有所帮助。

以上就是【2022年省考行测数量之《几何最值理论之平面图形》】的相关介绍，如果要了解更多热门资讯，欢迎关注吉林华图教育。