2022年行测备考:“最”翁之意——你多我少,如此分配刚刚好
2022-02-04 13:36 吉林公选遴选考试 来源:未知
2022年行测备考:“最”翁之意——你多我少,如此分配刚刚好
在数量关系中有一种题型称之为“数列构造”,相信参加过公考的同学或者有过备考经历的同学对这种题型并不陌生。虽然该题型考查频率并不高,但是题型之趣味让同学们在数量关系的课堂上找到了自信与乐趣。对于这种考查频率较低但简单有趣的题型,建议备考时抓住考查的核心知识点,在尽可能短的时间内理解考查的要素,做到高效率备考,那么接下来我们来学习数列构造的解题技巧。
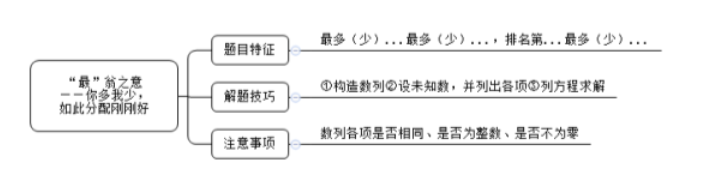
题型特征:最多(少)......最多(少)......,排名第......最多(少)......
解题技巧:①构造数列②设未知数,并列出各项③列方程求解
考查情景一:数列各项不相同,且为整数
【例题】在一次竞标中,评标小组对参加竞标的公司进行评分,满分120分。按得分排名,前5名的平均分为115分,且得分是互不相同的整数,则第三名得分至少是( )。
A.112分 B.113分
C.115分 D.116分
【答案】B
【解析】第一步,前5名的总分为,假设第三名的分数为x,由于总分是一定的,为使第三名的分数尽可能少,那么其他4名的分数则尽可能多一些,但要保证每一个的分数是整数且不同。
第二步,为满足上述要求,假设第一名和第二名的分数依次为120、119,第四名和第五名的分数应尽可能高,但应比第三名少,因此分数依次为x-1、x-2。
第三步,利用总分是定值进行列方程,120+119+x+(x-1)+(x-2)=575,解得x=113。
因此选择B选项。
考查情景二:数列各项允许出现相同,同时要求为整数
【例题】某单位2011年招聘了65名毕业生,拟分配到该单位的7个不同部门。假设行政部门分得的毕业生人数比其他部门都多,问行政部门分得的毕业生人数至少为( )名。
A.10 B.11
C.12 D.13
【答案】B
【解析】第一步,总人数是65人,假设行政部门的人数为x,为满足题目条件,那么其他部门的人数应比行政部门少,但又尽可能多一些。
第二步,由于题目没有限制其他部门人数不相同,因此其他部门的人数最多都可以表示为x-1。
第三步,利用总人数列方程,x+6(x-1)=65,解得x≈10.1。由于x取正整数,因此x的最小值为11。
因此选择B选项。
总体来看,数列构造这类考题在形式上会出现求某个量的最大值或最小值,在方法上选择列方程这种简单有效的解题方法。实质上这类考题的本质是:总量是定值,对不同对象进行分配,我们需要寻求分配的极限值。这样来看的话,遵循“你多我少”是一个基本原则。其次注意分配过程中各个对象的分配是否相同,这决定了其他分配对象的极值。由于数据较大分配对象较多,所以很难快速看出分配的结果,因此采用列方程就可以有效解决问题。希望各位考生在备考数列构造这类考题时多使用构造的思想,用数学方法和思维去解决问题,这就是“最”翁之意!

贴心微信客服


 华图优品
华图优品  助你上岸
助你上岸 招考资讯
招考资讯 图书教材
图书教材










