2022-01-28 09:53:54 吉林公务员考试网 jl.huatu.com 文章来源:华图教育
公务员行测备考:用最小公倍数巧解植树问题
植树问题,顾名思义,即涉及到植树类的题目,包含直线单侧植树、两侧植树、楼间植树与环形植树。当然,不仅仅是单一的植树,安装路灯、摄像头、挖洞插旗杆等间隔一定距离工作的类型都属于植树问题,需要用植树的思维去解答。
解题思路
首先掌握基础知识:

再考查植树与最小公倍数的关系:
例如,一段固定长度的街道,原来每隔5米种一棵树,说明每棵树所在的位置为5的整数倍,后面改为4米一棵树,说明之后每棵树所在的位置为4的整数倍,那么如果有某些位置既是5的整数倍,又是4的整数倍,即5和4的公倍数,这些位置的树就不需要挪动,这些位置和5、4的最小公倍数相关,整段路有多少个这样的公倍数,就有几个位置已经在第一次的间隔中被种植或者安装,调整间隔种植时,不需要调整或移动,即不需要挪动的位置数=路长/前后距离的最小公倍数(注意计算直线路段不需要挪动树的棵数时依然要考虑加1或减1)。
思路运用
【例1】施工队给一个周长为40米的圆形花坛安装护栏,刚开始,每隔1米挖一个洞用于建栏杆。后来发现间隔太远,决定改为每0.8米挖一个洞。那么至少需要再挖( )个洞。
A.39
B.40
C.41
D.42
【答案】B
【解析】第一步,可知题目中涉及间隔一定距离工作,为植树问题;
第二步,环形挖洞的个数=40/0.8=50个洞,但由于之前已经存在了一些洞,若是洞重合,则无需再挖,之前每个洞所在的位置为1米的整数倍,之后每个洞所在的位置为0.8米的整数倍,则它们最小公倍数的位置是重合的,不需要再重新挖,共有40/10=10个洞重合(4为0.8米与1米的最小公倍数)。至少还需再挖50-10=40个洞。
因此,选择B选项。
【例2】某公园举办春节花展,在周长400米的中心区布置了环形花槽,并在花槽上每隔16米挂一只灯笼,不久后元宵灯会临近,公园决定增加并挪动一些灯笼,但仍保持灯笼间距相等。已知加入新灯笼后,共有5只旧灯笼没有移动,则调整后的灯笼间距最大为( )米。
A.12
B.10
C.8
D.5
【答案】B
【解析】第一步,根据题目意思,5只没有移动的灯笼把花槽分成5段,每段长为400÷5=80(米);
第二步,设增加一些灯笼后间距为x米,原间距是16米,没有移动的灯笼间距为两次加入灯笼间距的最小公倍数,则16与x的最小公倍数为80。代入选项,只有B、D选项两个数字与16的最小公倍数为80。题目要求间隔最大,则增加灯笼后的间距为10米。
因此,选择B选项。
通过上述两个植树问题与最小公倍数综合考查的题目不难发现,在植树问题中,涉及到前后两次间隔距离调整,那么两个距离公倍数的位置不需要再重新操作。不管是正面还是反面考查,只有将其原理掌握,才能一举拿下。
思路总结
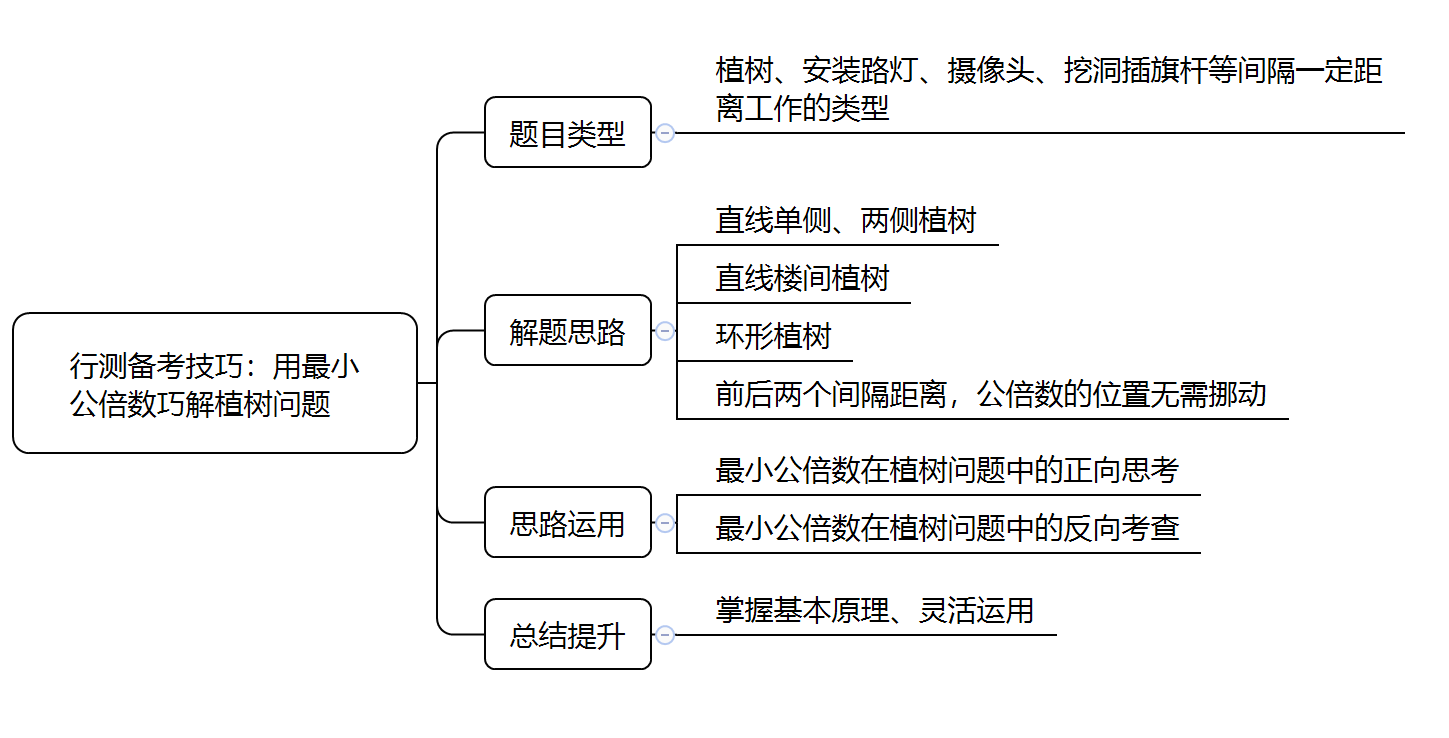
以上就是【公务员行测备考:用最小公倍数巧解植树问题】的相关介绍,如果要了解更多热门资讯,欢迎关注吉林华图教育。

贴心微信客服
下一篇:没有了