2022公务员行测备考技巧：几何问题特殊解法之赋值法巧解

2022公务员行测备考技巧：几何问题特殊解法之赋值法巧解

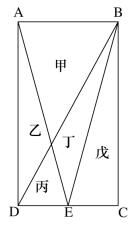
　　一块种植花卉的矩形土地如图所示，AD边长是AB的2倍，E为CD边的中点，甲、乙、丙、丁、戊区域分别种植白花、红花、黄花、紫花、白花。问种植白花的面积占矩形土地面积的：

　　A.3/4

　　B.2/3

　　C.7/12

　　D.1/2

　　解析：根据题目信息可知，本题考查几何问题，题目中未给出具体的数据，只给出对应花卉种植面积之间的关系，问题涉及对应花卉的占比，可以采用赋值法解。由图形面积关系可以赋值丙面积为1，根据“AD边长是AB的2倍，E为CD边的中点”得到AB=2DE，所以甲的面积为4(几何特性：相似图形，面积之比等于边长之比的平方)。丙和丁的底边都在DB上，顶点都为E，由于高相同，三角形面积比等于底边长之比，故得到丁的面积为2，同理可得乙的面积也为2。由于戊的面积与丙、丁面积之和相等(三角形底边长度相等，高相等)，所以戊的面积为3，矩形总面积为4+2+1+2+3=12。根据种白花的面积为4+3=7，得到白花面积的占比为。选择C选项。

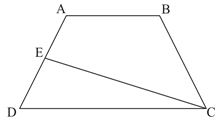
　　如下图，ABCD是一个梯形，E是AD的中点，直线CE把梯形分成甲、乙两部分，其面积之比为5∶2，那么上底AB与下底CD的长度之比是()。

　　A.2∶5

　　B.3∶5

　　C.3∶4

　　D.4∶7

　　解析：根据题目信息可知本题考查几何问题，根据题目信息本题未给出具体数值，只给出甲乙面积之比，问的是上底与下底长度之比，故可用赋值法解。根据甲、乙面积之比是5∶2，赋值甲、乙的面积分别为5和2。如下图所示：连接CA，根据E为AD“中点”知，△ACE和△CDE等底、等高，乙的面积为2，则△ACE的面积也为2，△ABC的面积为5-2=3。△ABC和△ACD等高、底不同，底分别为AB、DC，则三角形面积之比等于底边之比。选择C选项。

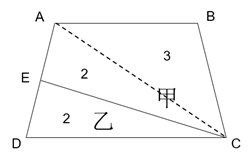
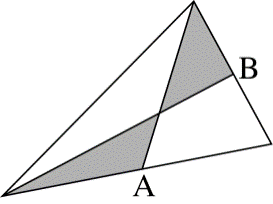
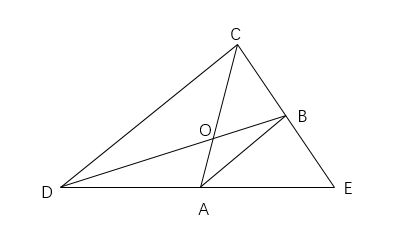
　　如图三角形中，A、B分别为两条边的中点，则图中阴影部分面积为三角形总面积的()。

　　A.1/3

　　B.1/4

　　C.2/7

　　D.3/8

　　解析

　　：根据题目信息可知本题考查几何问题。题目中未给具体数值，可考虑用赋值法解，连接AB。根据图形信息可知，如下图所示，连接AB并在图中标上对应字母，A、B分别为CE和DE两条边的中点,赋值△CDE面积为1，△BCD的面积占△CDE的

　　，△ABD的面积占△DBE的

　　解析：根据题目信息可知本题考查几何问题。题目中未给具体数值，可考虑用赋值法解，连接AB。根据图形信息可知，如下图所示，连接AB并在图中标上对应字母，A、B分别为CE和DE两条边的中点,赋值△CDE面积为1，△BCD的面积占△CDE的，△ABD的面积占△DBE的，所以△ABD的面积占△CDE的，故△BCD的面积是△ABD的面积的2倍，则有OC∶OA=2∶1。，那么△AOD的面积占总面积的，△BOC的面积占总面积的×=，那么阴影面积(△AOD和△BOC)占总面积(△CDE)的比值为。

　　，所以△ABD的面积占△CDE的

　　解析：根据题目信息可知本题考查几何问题。题目中未给具体数值，可考虑用赋值法解，连接AB。根据图形信息可知，如下图所示，连接AB并在图中标上对应字母，A、B分别为CE和DE两条边的中点,赋值△CDE面积为1，△BCD的面积占△CDE的，△ABD的面积占△DBE的，所以△ABD的面积占△CDE的，故△BCD的面积是△ABD的面积的2倍，则有OC∶OA=2∶1。，那么△AOD的面积占总面积的，△BOC的面积占总面积的×=，那么阴影面积(△AOD和△BOC)占总面积(△CDE)的比值为。

　　，故△BCD的面积是△ABD的面积的2倍，则有OC∶OA=2∶1。，那么△AOD的面积占总面积的

　　解析：根据题目信息可知本题考查几何问题。题目中未给具体数值，可考虑用赋值法解，连接AB。根据图形信息可知，如下图所示，连接AB并在图中标上对应字母，A、B分别为CE和DE两条边的中点,赋值△CDE面积为1，△BCD的面积占△CDE的，△ABD的面积占△DBE的，所以△ABD的面积占△CDE的，故△BCD的面积是△ABD的面积的2倍，则有OC∶OA=2∶1。，那么△AOD的面积占总面积的，△BOC的面积占总面积的×=，那么阴影面积(△AOD和△BOC)占总面积(△CDE)的比值为。

　　，△BOC的面积占总面积的

　　解析：根据题目信息可知本题考查几何问题。题目中未给具体数值，可考虑用赋值法解，连接AB。根据图形信息可知，如下图所示，连接AB并在图中标上对应字母，A、B分别为CE和DE两条边的中点,赋值△CDE面积为1，△BCD的面积占△CDE的，△ABD的面积占△DBE的，所以△ABD的面积占△CDE的，故△BCD的面积是△ABD的面积的2倍，则有OC∶OA=2∶1。，那么△AOD的面积占总面积的，△BOC的面积占总面积的×=，那么阴影面积(△AOD和△BOC)占总面积(△CDE)的比值为。

　　解析：根据题目信息可知本题考查几何问题。题目中未给具体数值，可考虑用赋值法解，连接AB。根据图形信息可知，如下图所示，连接AB并在图中标上对应字母，A、B分别为CE和DE两条边的中点,赋值△CDE面积为1，△BCD的面积占△CDE的，△ABD的面积占△DBE的，所以△ABD的面积占△CDE的，故△BCD的面积是△ABD的面积的2倍，则有OC∶OA=2∶1。，那么△AOD的面积占总面积的，△BOC的面积占总面积的×=，那么阴影面积(△AOD和△BOC)占总面积(△CDE)的比值为。

　　=，那么阴影面积(△AOD和△BOC)占总面积(△CDE)的比值为

　　解析：根据题目信息可知本题考查几何问题。题目中未给具体数值，可考虑用赋值法解，连接AB。根据图形信息可知，如下图所示，连接AB并在图中标上对应字母，A、B分别为CE和DE两条边的中点,赋值△CDE面积为1，△BCD的面积占△CDE的，△ABD的面积占△DBE的，所以△ABD的面积占△CDE的，故△BCD的面积是△ABD的面积的2倍，则有OC∶OA=2∶1。，那么△AOD的面积占总面积的，△BOC的面积占总面积的×=，那么阴影面积(△AOD和△BOC)占总面积(△CDE)的比值为。

以上就是【2022公务员行测备考技巧：几何问题特殊解法之赋值法巧解】的相关介绍，如果要了解更多热门资讯，欢迎关注吉林华图教育。