2021-12-17 08:48:22 吉林公务员考试网 jl.huatu.com 文章来源:华图教育
2023年松原国考行测备考:轻松掌握排列组合之捆绑法
很多同学在备考的过程中都觉得排列组合是个硬骨头,不想花费时间,遇到了就直接跳过。其实排列组合有很多方法和技巧,如果熟练掌握,做起来也不麻烦。接下来给大家讲解排列组合的一种解题技巧—捆绑法。
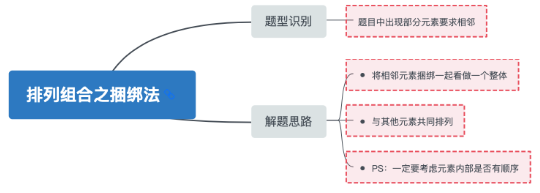
首先我们先来了解,捆绑法什么时候用:当排列组合题目中出现部分元素要求相邻。解题方法:将要求相邻元素捆绑在一起看做一个整体,然后与其他元素共同排列(一定要考虑被捆绑的元素内部是否有顺序)。接下来我们来看几道例题:
【例1】有两对夫妇各带一个小孩乘坐有6个座位的游览车,游览车每排只有1个座位。为安全起见,车的首尾两座一定要坐两位爸爸;两个小孩一定要排在一起。那么,这6人的排座方法有多少种?
A.12种 B.24种
C.36种 D.48种
【答案】B
【解析】第一步,本题考查排列组合问题,属于方法技巧类,用捆绑法解题。
第二步,先将两位爸爸安排在首尾两座,有(种)方法;再将两个小孩看成一个整体,与两位妈妈一起排列,有(种)方法。
第三步,6人的排座方法共有2×12=24(种)方法。
因此,选择B选项。
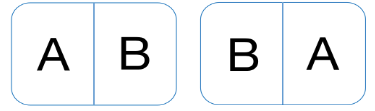
在这里同学们一定要注意,捆绑的元素内部是否有顺序,两个孩子是两个元素,我们用字母A和B来表示,A在左边B在右边和A在右边B在左边是完全不同的两种情况,所以捆绑的元素内部要进行再排序,
【例2】某场科技论坛有5G、人工智能、区块链、大数据和云计算5个主题,每个主题有2位发言嘉宾。如果要求每个主题的嘉宾发言次序必须相邻,问共有多少种不同的发言次序?
A.120 B.240
C.1200 D.3840
【答案】D
第一步,本题考查排列组合问题,用捆绑法解题。
第二步,先把每个主题的2个人捆绑在一起,形成5个整体进行排列,有(种)排列方式,每个整体内部是2个人,有2种排列方式。故共有(种)发言次序。
因此,选择D选项。
【例3】某美术馆计划展出12幅不同的画,其中有3幅油画、4幅国画、5幅水彩画,排成一行陈列,要求同一种类的画必须连在一起,并且油画不放在两端,问有多少种不同的陈列方式?
A.不到一万种 B.1万-2万种之间
C.2万-3万种之间 D.超过3万种
【答案】D
【解析】第一步,本题考查排列组合问题,用捆绑法解题。
第二步,3幅油画捆绑在一起,4幅国画捆绑在一起,5幅水彩画捆绑在一起,一共3个整体,但是油画不能在两端,则油画必须在中间,那么国画和水彩画在两端有(种)方式,3幅油画内部有(种)方式,4幅国画内部有(种)方式,5幅水彩画内部有(种)方式,那么一共有2×6×24×120=34560>30000(种)。
因此,选择D选项。
通过上面三道题目的讲解,相信同学们对于捆绑法有了基本的认识与了解,我们只要能够识别题型,直接套用解题方法也并不难。相信以后再遇到此类题目的时候大家都能快速做出来。
思维导图
以上就是【2023年松原国考行测备考:轻松掌握排列组合之捆绑法】的相关介绍,如果要了解更多热门资讯,欢迎关注吉林华图教育。

贴心微信客服