2021-12-16 19:46:46 吉林公务员考试网 jl.huatu.com 文章来源:通化华图
职测之数量关系:鸡兔同笼问题
在职测考试的复习过程中,数量关系一直是令大家比较难受的模块。但,职测中的鸡兔同笼问题还是经常常见,而且比较好把握的,那今天我们就来看看鸡兔同笼问题。
一、什么是鸡兔同笼问题
鸡兔同笼是中国古代的数学名题之一。 大约在1500年前,《孙子算经》中就记载了这个有趣的问题。鸡兔同笼问题本质是特殊二元一次方程。那我们来探究下鸡兔同笼问题:
二、鸡兔同笼问题例题
有若干只鸡兔同在一个笼子里,从上面数,有35个头,从下面数,有94只脚。问笼中各有多少只鸡和兔?
三、鸡兔同笼问题的常用解法
鸡兔同笼问题的常用方法有:方程法、假设法。那我们就用这两种方法来解一下例题。
(1)方程法:设鸡有x只,兔子有y只,则有等量关系鸡跟兔子加起来共35个头;鸡的脚数量加兔子的脚数量等于94只:
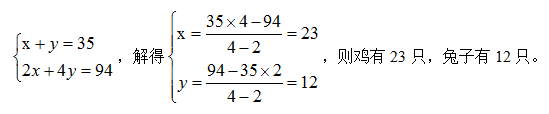
(1)假设法:
假设全是鸡:2 (只脚/只动物)× 35(只动物) = 70 (只脚)(严格按照量纲一致原则标注就如上所示。小学阶段只要求标出只,以下按此操作。),鸡脚比总脚数少:94 - 70 = 24 (只)。兔子比鸡多的脚数:4 - 2 = 2(只),兔子的只数:24 ÷ 2 = 12 (只)鸡的只数:35 - 12 = 23(只)。
假设全是兔子:4 × 35 = 140(只),兔子脚比总数多:140 - 94 = 46(只),兔子比鸡多的脚数:4 - 2 = 2(只),鸡的只数:46 ÷ 2 = 23(只),兔子的只数:35 - 23 = 12(只)。
综上,两种解法我们可以发现,其实假设法的本质就是解二元一次方程的,用假设法解题是解方程的步骤。
四、鸡兔同笼问题如何识别

那我们就把这类题型称为鸡兔同笼问题。用文字来描述就是要已知两个和:1.多个主体的和;2.多个主体与其系数相乘相加的和。
五、鸡兔同笼问题的常见题型
例:老师在课堂上出了18个题,规定学生答对一题得6分,答错一题倒扣一分,一个学生全部做完后得94分,问他答对了多少题?
A.12 B.14 C.16 D.17
解析:选C。根据题干,1.多个主体的和,答对的题目数加答错的题目数等于18题;2.多个主体与其系数相乘相加的和,对的题目总分加错的题目总分是94分,则是鸡兔同笼问题。假设法解题,设18个题全部答对,则分数为18×6=108分,现在实际的分数为94分,则需要少14分,每一个答对的题目变成答错的题目,少7分,因此需要有14÷7=2道答错的题,因此答对的题目数为18-2=16道,故选C。
例:20人乘飞机从甲市前往乙市,总费用为27000元。每张机票的全价票单价为2000元,除全价票之外,该班飞机还有九折票和五折票两种选择。每位旅客的机票总费用除机票价格之外,还包括170元的税费。则购买九折票的乘客与购买全价票的乘客人数相比为( )
A.一样多 B.买九折票的多1人
C.买全价票的多2人 D.买九折票都多4人
解析:选A。根据题干,20个人坐飞机,已知了多个主体的和;总费用27000元,减去每张票的税费,则总机票钱为23600元,这是多个主体与其相乘相加的和,则这个题是鸡兔同笼问题。假设20张机票全是5折票,则总机票钱为20×2000×0.5=20000元,实际的机票费用为23600,则需要多出来3600元。每一张五折票1000元变成全价票2000元,则需要多出来1000元,有多少全价票不清楚,假设全价票有x张;每一张五折票1000元变成九折票1800元,则需要多出来800元,有多少九折票不清楚,假设九折票有y张。得1000x+800y=3600,x、y都是正整数则,x=2,y=2,选A。
更多备考资料欢迎电话咨询:0435-3500222
以上就是【职测之数量关系:鸡兔同笼问题】的相关介绍,如果要了解更多热门资讯,欢迎关注吉林华图教育。

贴心微信客服
上一篇:职测之数量关系:解利润用列表
下一篇:没有了