2021-11-10 10:49:30 吉林公务员考试网 jl.huatu.com 文章来源:镇赉华图
行测考试数量关系之轻松搞定容斥原理-镇赉华图
容斥原理是行测考试中的一类常考题型,常见的容斥原理涉及两集合容斥原理和三集合容斥原理。这类题型特征明显,方法固定,属于易拿分的题型,接下来给大家分享一下容斥原理的做题方法。
一、题型特征
题目的条件中出现“都满足”或者“都不满足”,其本质是找到并去除重复的过程。
二、解题技巧
①公式法
两集合容斥原理:总个数-两者都不满足的个数=A+B-AB。其中A、B分别代表满足不同条件的数量,AB代表两个条件都满足的数量。
三集合容斥原理标准型:总个数-都不满足的个数=A+B+C-AB-BC-AC+ABC。其中A、B、C代表满足不同条件的数量,AB、BC、AC代表分别满足其中两个条件的数量,ABC代表三个条件都满足的数量。
三集合容斥原理非标准型:总个数-都不满足的个数=A+B+C-只满足两个条件的数量-2×ABC。
②画图法
操作方法:画图——标注条件——找面积相等。适用于所有的容斥问题,特别地,当题目中出现“只满足”或者“仅满足”时,画图法最适合,且标注数据时从中心向外逐次标注。
三、例题精讲
【例1】运动会上100名运动员排成一列,从左向右依次编号为1-100,选出编号为3的倍数的运动员参加开幕式队列,而编号为5的倍数的运动员参加闭幕式队列。问既不参加开幕式又不参加闭幕式队列的运动员有多少人?( )
A.46 B.47
C.53 D.54
【答案】C
【解析】问题中出现“既不…也不…”,属于两集合容斥类。编号为3的倍数的运动员有100÷3=33…1,即33位,编号为5的倍数的运动员有100÷5=20位。编号既是3又是5的倍数(即15的倍数)的运动员有100÷15=6…10,即6位。根据两集合公式,100-既不参加开幕式也不参加闭幕式的运动员=33+20-6,利用尾数法,可得既不参加开幕式也不参加闭幕式的运动员的数量为53。因此,本题选择C选项。
【例2】对39种食物中是否含有甲、乙、丙三种维生素进行调查,结果如下:含甲的有17种,含乙的有18种,含丙的有15种,含甲、乙的有7种,含甲、丙的有6种,含乙、丙的有9种,三种维生素都不含的有7种,则三种维生素都含的有多少种?( )
A.4 B.6
C.7 D.9
【答案】A
【解析】题目中出现“含甲、乙;含甲、丙;含乙、丙”,应使用三集合标准型公式:17+18+15-(7+6+9)+三种维生素都含=39-7,利用尾数法,可得三种维生素都含的数量为4。因此,本题选择A选项。
【例3】某企业调查用户从网络获取信息的习惯,问卷回收率为90%。调查对象中有179人使用搜索引擎获取信息,146人从官方网站获取信息,246人从社交网站获取信息,同时使用这三种方式的有115人,使用其中两种的有24人,另有52人这三种方式都不使用。问这次调查共发出了多少份问卷?( )
A.310 B.360
C.390 D.410
【答案】D
【解析】题目中出现“使用三种方式、使用两种方式”,应使用三集合容斥原理的非标准型公式:179+146+246-24-2×115=总人数-52,解得总人数为369,故问卷数量为369÷90%=410。因此,本题选择D选项。
【例4】联欢会上,有24人吃冰激凌、30人吃蛋糕、38人吃水果,其中45既吃冰激凌又吃蛋糕的有12人,既吃冰激凌又吃水果的有16人,既吃蛋糕又吃水果的有18人,三样都吃的则有6人。假设所有人都吃了东西,那么只吃一样东西的人数是多少?( )
A.12 B.18
C.24 D.32
【答案】B
【解析】问题中出现“只吃一样”,所以使用画图法,并注意从中心往外逐次计算标数:
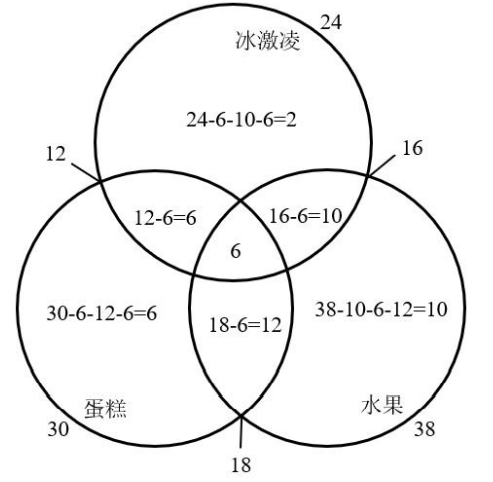
由图所示,只吃一样东西的有2+6+10=18(人)。因此,本题选择B选项。
以上就是对容斥原理知识的讲解,大家一定要牢记此类题型的特征以及方法,多加练习,只有这样,才能在考场上迅速辨认出来,并拿下这类题型的分。
以上就是【行测考试数量关系之轻松搞定容斥原理-镇赉华图】的相关介绍,如果要了解更多热门资讯,欢迎关注吉林华图教育。

贴心微信客服