2022国家公务员考试每日一练解析6

　　1.(单选题)某机关开展红色教育月活动，三个时间段分别安排了三场讲座。该机关共有139人，有42人报名参加第一场讲座，51人报名参加第二场讲座，88人报名参加第三场讲座，三场讲座都报名的有12人，只报名参加两场讲座的有30人。问没有报名参加其中任何一场讲座的有多少人?

　　A.12

　　B.14

　　C.24

　　D.28

　　解析

　　第一步，本题考查容斥原理，用公式法解题。

　　第二步，设没有报名参加其中任何一场讲座的有x人。根据三集合非标准型容斥原理公式，可列方程42+51+88-30-2×12=139-x，解得x=12。(或者使用尾数法解题)

　　因此，选择A选项。

　　2.(单选题)某单位男女员工的人数之比是15∶13。按人数之比5∶7∶8，分为甲、乙、丙三个科室。其中甲科室男女员工的人数之比为4∶3，乙科室为5∶2。则丙科室男女员工人数之比为：

　　A.1∶2

　　B.2∶3

　　C.5∶9

　　D.5∶8

　　解析

　　第一步，本题考查基础应用题，用赋值法解题。

　　第二步，根据男女比为15∶13，则总人数应该为28的倍数;又因为甲∶乙∶丙=5∶7∶8，则总人数应该为20的倍数;所以赋值总人数为140，则男生人数为75，女生人数为65。甲=35，乙=49，丙=56。又因为甲科室的男女比为4∶3，则甲的男生为20，甲的女生为15，又因为乙科室的男女比为5∶2，则乙的男生为35，乙的女生为14，所以得出丙的男生为75-20-35=20，丙的女生为65-15-14=36，则丙的男女比=20∶36=5∶9。

　　因此，选C选项。

　　4.(单选题)某单位购买了10台新电脑，计划分配给甲、乙、丙3个部门使用。已知每个部门都需要新电脑，且每个部门最多得到5台，那么电脑分配方法共有( )种。

　　A.9

　　B.12

　　C.18

　　D.27

　　解析

　　第一步，本题考查排列组合问题。

　　5.(单选题)某个项目由甲、乙两人共同投资，约定总利润10万元以内的部分甲得80%，10万元—20万元的部分甲得60%，20万元以上的部分乙得60%。最终乙分得的利润是甲的1.2倍。问如果总利润减半，甲分得的利润比乙：

　　A.少1万元

　　B.少2万元

　　C.多1万元

　　D.多2万元

　　解析

　　第一步，本题考查经济利润问题，属于分段计费类。

　　第二步，利润分得方式分为三段：①0—10万元的部分甲分得8万元，乙分得2万元;②10—20万元的部分甲分得6万元，乙分得4万元;③设超过20万元的部分为x万元，则甲分得0.4x万元，乙分得0.6x万元。

　　第三步，甲获得的总利润是8+6+0.4x，乙获得的总利润是2+4+0.6x，由题意1.2×(8+6+0.4x)=2+4+0.6x，解得x=90。

　　第四步，总利润是20+90=110(万元)，减半是55万元，则甲分得8+6+(55-20)×0.4=28(万元)，乙分得2+4+(55-20)×0.6=27(万元)。甲比乙多1万元。

　　因此，选择C选项。

　　6.(单选题)企业对25名应聘者进行面试。已知所有应聘者的能力都不相同，面试采取5人一组的无领导小组讨论形式，每次面试都能对小组内5个人的能力进行排名。问至少要进行多少次面试才能保证选出能力最强的4个人?

　　A.7

　　B.8

　　C.9

　　D.10

　　解析

　　第一步，本题考查最值问题，属于最不利构造。

　　第二步，首先将25个人分成A、B、C、D、E五个小组进行无领导小组讨论，按每个人的能力水平排序，进行五场得到如下表格：

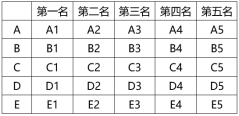
　　第三步，将每组第一名五个人进行小组讨论，这样可以评选出25人中的第一名。在此假定为按能力水平从大到小排序分别是A1>B1>C1>D1>E1，进行一场即第六场能确定A1是25人中的第一名。

　　第四步，将有可能是第二名或第三名的人放在一个小组进行评选，由于A1>B1>C1>D1，C组后四名、D组和E组都不可能出二三名，第二名只能是A2或者B1，第三名只能是A2、A3、B1、B2或者C1。那么将A2、B1、A3、B2、C1五个人进行评选，进行一场即第七场能确定第二名和第三名。

　　第五步，第七场排名可能情况如下：

　　①A2能力最好，B1其次。第四名只能是A3、B2、C1中的一个，恰好都在本场中，那么这7场已经全部搞定前四名。

　　②A2能力最好，A3其次。那么第四名只能是B1或者A4，将两人同时放到一场讨论即可知道谁是25人中的第四名，一共需要8场。

　　③B1能力最好，A2其次。第四名只能是A3、B2、C1中的一个，恰好都在本场中，那么这7场已经全部搞定前四名。

　　④B1能力最好，B2其次。如果C1>A2，那么第四名只能是B3或者C1，将两人同时放到一场讨论即可知道谁是25人中的第四名，一共需要8场;如果C1

　　⑤B1能力最好，C1其次。如果接下来A2>B2，那么第四名可能是A2、C2、D1，将三人同时放到一场讨论即可知道谁是25人中的第四名，一共需要8场;如果接下来B2>A2，那么第四名可能是B2、C2、D1，将三人同时放到一场讨论即可知道谁是25人中的第四名，一共需要8场。

　　综上所述，8场就可以选出前四名。

　　因此，选择B选项。

　　7.(单选题)球员小王与球队签订工作合同，有1年期、3年期和5年期三种合同可供选择。如果签3年期合同，月薪比5年期合同低1万元，比1年期高5000元，而5年合同能获得的总薪水是3年期合同的2.5倍。问小王如果签1年期合同，能获得的总薪水为多少万元?

　　A.12

　　B.18

　　C.24

　　D.30

　　解析

　　第一步，本题考查基础应用题，用方程法解题。

　　第二步，设签3年的月薪为x万元，则签5年的月薪为(x+1)万元，签1年的月薪为(x-0.5)万元。可列方程：3×12x×2.5=5×12×(x+1)，解得x=2，那么签1年的月薪是1.5万元，年薪是1.5×12=18(万元)。

　　因此，选择B选项。

　　8.(单选题)在ATM机上输入银行卡密码时，若连续三次输入错误则会吞卡，老李忘了银行卡密码的末两位数，只记得是两个不相同的奇数，若他在末两位上随意输入两个不同奇数，能在吞卡前猜中正确密码的概率是：

　　9.(单选题)出租车的起步价是2公里7元，往后每增加1公里车费增加2.6元，若不足1公里按1公里计费。某人从甲地到乙地乘坐出租车共支付车费20元，如果从甲地到乙地先步行800米，然后再乘坐出租车也是20元，那么乘出租车从甲、乙两地中点到乙地需要支付车费()元。

　　A.9.6

　　B.14.8

　　C.12.2

　　D.7

　　解析

　　第一步，本题考查经济利润问题。

　　第二步，车费一共20元，起步价是7元，走了2公里，超出20-7=13(元)，走了13÷2.6=5(公里)，若先步行0.8公里车费仍然为20元，说明总里程介于6.8—7公里，到甲乙中点的路程在3.4—3.5之间，应按4公里收车费，车费为7+2×2.6=12.2(元)。

　　因此，选择C选项。

　　10.(单选题)箱子里有乒乓球和网球若干，若每次取出乒乓球2个，网球1个，若干次后正好都取完;若每次取出乒乓球5个，网球3个，则网球取尽后，还剩余5个乒乓球，那么乒乓球和网球共有多少个?

　　A.40

　　B.45

　　C.53

　　D.58

　　解析

　　解法一：

　　第一步，本题考查基础应用题，用方程法解题。

　　第二步，设两种方式各取x、y次，第一次乒乓球、网球分别取出2x、x个;第二次乒乓球、网球分别取出5y+5、3y，根据乒乓球和网球的数量不变可得2x=5y+5、x=3y，联立方程解得y=5，x=15。

　　第三步，故乒乓球和网球共有2x+x=3x=15×3=45(个)。

　　因此，选择B选项。

　　解法二：

　　第一步，本题考查基础应用题，用代入排除法解题。

　　第二步，根据每次取乒乓球2个、网球1个且若干次后正好取完，可知乒乓球与网球的个数比为2∶1，故总球数为3的倍数，排除A、C、D选项。

　　因此，选择B选项。

 

网课学习—— 华图优品

面授课程—— 助你上岸

招考公告—— 招考资讯

图书推荐—— 图书教材