2021-11-04 09:23:19 吉林公务员考试网 jl.huatu.com 文章来源:通榆华图
国考行测数量关系:如何让不定方程组变easy
对于公考行测科目中数量关系的部分,不定方程(组)的问题是经常出现的,值得引起重视。过去我们经常接触的基础应用题大多为一元一次方程或者二元一次方程组等,而对于不定方程(组)接触的相对比较少,其实在公考中的不定方程(组)都是相对简单的,对于不定方程(组)我们也有一个完整的解题思路来解决这类问题。大家都知道含有未知数的等式,并把两个或两个以上等式联立称之为方程组。今天就跟着小编一起学习一下不定方程组中的问题吧,相信大家只要耐心细心,就会对解决不定方程组问题充满信心。
下面就和小编一起来了解一下不定方程组的相关知识点吧:
首先,我们要知道什么是不定方程组?
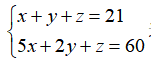
不定方程组是指未知数的个数多于方程个数,例如:这样的方程组,未知数个数有三个,方程个数有两个,这种未知数个数大于方程个数的方程组就是不定方程组。
其次,当我们根据题意列出了不定方程组,该如何解决?记住这两步:
第一步,加减消元或代入消元得到一个不定方程。注意:在消元时不仅要保留所求的未知数,而且要寻求简单未知数进行消元。
第二步,消元后将不定方程组化为不定方程,在确定不定方程中未知数的值时,方法有:
①代入排除法:求的是单个未知数的题时可以用这个方法;
②数字特性法:奇偶特性、倍数特性、尾数特性;
③赋“0”法;
下面我们通过一道例题来实际应用一下刚才所学的知识点吧!
【例题】某次田径运动会中,选手参加各单项比赛计入所在团体总分的规则为:一等奖得9分,二等奖得5分,三等奖得2分。甲队共有10位选手参赛,均获奖。现知甲队最后总分为61分,问该队最多有几位选手获得一等奖?
A. 3 B. 4
C. 5 D. 6
这道题选C选项,小伙伴们,选对了么?没选对的小伙伴,我们一起来看看如何解这道不定方程组题吧!
拿到题,先根据题干信息以及问题,来判定一下题型,本题可以确定为基础应用题。
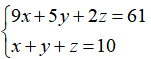
判定完题型,我们来仔细阅读题干,可以发现两个等量关系:①获得一等奖,二等奖,三等奖的总人数为总人数10人;②获得一等奖,二等奖,三等奖的总分数为甲队总分61分。根据这两个等量关系我们可以列出两个等式,然而我们发现题中没有给出获得一等奖,二等奖,三等奖的人数,且获得一等奖的人数为我们要求的答案。我们可以设获得一等奖的人数为x人,获得二等奖的人数为y人,获得三等奖的人数为z人。那么,我们就可以得到一个方程组。很明显两个方程三个未知数,未知数个数大于方程个数,这是一个不定方程组。下面我们根据刚刚讲述的解题步骤来做:第一步,加减消元保留x得到不定方程7x+3y=41;第二步,本题是求的一个未知数,那么可以利用代入排除法解题,题中问的是最多,那么从四个选项中最大的开始代入。代入D选项,得,解出为负值且不是整数,所以D选项不符合题意,排除。代入C选项,得,C选项符合题意,因此选择C选项。
小伙伴们是不是很简单,下次遇见它记得这两步方法哦!
【解题思路】
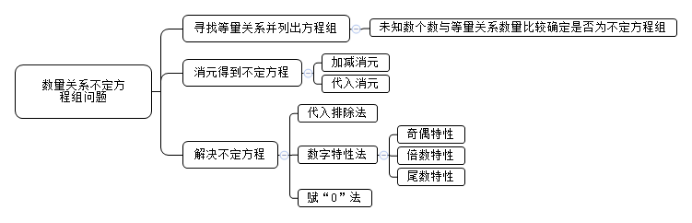
以上就是【国考行测数量关系:如何让不定方程组变easy】的相关介绍,如果要了解更多热门资讯,欢迎关注吉林华图教育。

贴心微信客服
上一篇:国考真假推理中的矛盾关系
下一篇:没有了