2021-10-14 19:02:51 吉林公务员考试网 jl.huatu.com 文章来源:通榆华图
公务员行测数量关系:几何特性之等比例放缩
一、知识概览
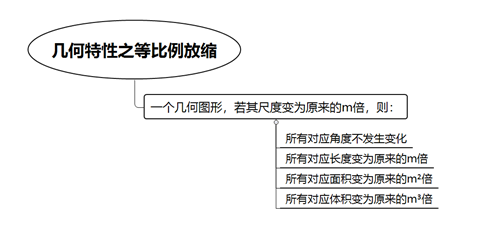
等比例放缩,也叫尺度扩大理论,是相似图形中求边长、周长、面积或体积的常见方法。一个几何图形,若其尺度变为原来的m倍,则:所有对应角度不发生变化;所有对应长度变为原来的m倍;所有对应面积变为原来的m²倍;所有对应体积变为原来的m³倍。
例如:一个正三角形和一个正六边形周长相等,则正六边形面积为正三角形的( )倍。
【点拨】正三角形和正六边形周长相等,故边长之比为2∶1。将正六边形分割成如图所示的6个小正三角形,大正三角形与小正三角形的边长比为2∶1,根据等比例放缩(若其尺度变为原来的m倍,对应面积变为原来的m²倍),面积比为4∶1。
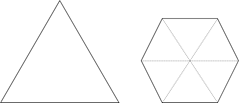
第三步,正六边形与正三角形的面积比为(6×1)÷4=1.5,即正六边形面积为正三角形的1.5倍。
二、例题精析
【例1】(2021国考)
在一块下图所示的梯形土地中种植某种产量为1.2千克/平方米的作物。已知该梯形的高为100米,ABC、BCD和CDE为正三角形,且BAF和DEG的角度都是90度,问该土地的总产量为多少吨?
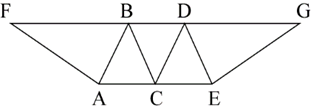

【答案】B
【解析】
第一步,本题考查几何问题,属于平面几何类。
第二步,由于中间三个三角形都是正三角形,可知∠ABF=60°,又∠BAF=90°,那么BF=2AB;边上两个直角三角形拼凑在一起是一个大正三角形且边长是小正三角形的2倍,根据等比例放缩(若其尺度变为原来的m倍,对应面积变为原来的m²倍)可知:大正三角形的面积是小正三角形面积的4倍。则整个图形是7个小正三角形的面积。

因此,选择B选项。
【例2】(2021国考)
一个人工湖的湖面上有一个露出水面3米的圆锥体人工景观(底面朝下)。如人工湖水深减少20%,则该景观露出水面部分的体积将增加61/64。问原来的人工湖水深为多少米?
A.3.5 B.3.75
C.4.25 D.4.5
【答案】B
【解析】
第一步,本题考查几何问题,属于立体几何。
![]()
第二步,水深变化前后的圆锥体相似,前后体积比为1:(1+)=64:125,根据等比例放缩(若其尺度变为原来的m倍,对应体积变为原来的m³倍),圆锥前后的高度之比为4:5,原来是3米,则水深减少之后是米。前后水深减少了0.75米是人工湖水深的20%,那么人工湖水深为0.75÷20%=3.75米。
因此,选择B选项。
无论是平面图形还是立体图形,当存在等比例放缩或者尺度扩大时,可应用等比例放缩的性质快速求解。
【小结】
以上就是【公务员行测数量关系:几何特性之等比例放缩】的相关介绍,如果要了解更多热门资讯,欢迎关注吉林华图教育。

贴心微信客服
下一篇:没有了