不定方程题型之因子特性法
行测考试中数量模块一直流传着“一半做、一半蒙” 的说法。那么哪些题型能做，哪些题型短时间内做不出来，需要同学们做好辨别，一定要把好做的题拿到分数，把难做的题目大胆地蒙。针对每个人的基础和擅长的题型不同，可能每个人舍弃的题目也不一样。但是根据我多年的授课经验来看，大部分同学对一些简单的题目，例如工程问题、容斥问题和不定方程问题等相对简单的题目还是很容易能拿到分的。
今天主要给大家介绍一下巧用因子特性法解不定方程问题的题型，希望同学们快速掌握，以提高行测分数。在学习因子特性之前先了解一下不定方程的概念，不定方程指的就是未知数的个数大于等式的式子，例如3X+4Y=15(X和Y都是正整数)。所谓因子特性就是：在一个不定方程中，其中两项都含有某个共同的因子(这里的因子其实就是约数)，则另外一项也含有某个共同的因子。例如3X+4Y=15中(X和Y是正整数)，其中15和3X这两项都含有共同的因子3，则4Y也含有共同的因子3，那么Y为3的倍数;Y可以等于3、6、9...。当Y=3时，X=1，这样就能快速解出不定方程了。光说不练假把式，下面我们通过一道例题来进行说明。
【例1】(单选题)小张的孩子出生的月份乘以29，出生的日期乘以24，所得的两个乘积加起来刚好等于900。问孩子出生在哪一个季度?
A. 第一季度 B. 第二季度
C. 第三季度 D. 第四季度
【答案】D
【解析】本题考察不定方程问题。设月份为M，日期为N，根据题意可得29M+24N=900，本题式子比较容易得到，很多同学也非常想用奇偶特性解题。那我们来试一下，也就是900是个偶数，24M也是偶数。可得到29M也是偶数，推出M是个偶数，此时M可能是2、4、6、8、10、12，如果直接代入会很麻烦。此时我们就需要更换思路，观察29M+24N=900，其中900和24N两项中都含有共同的因子12，此时根据因子特性可得到29M也要含有12因子，则M为12的倍数，且M表示月份，则M=12。这样就能很快解出来答案为第四季度。
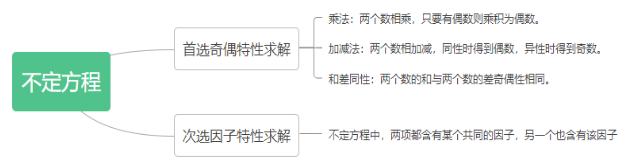
【总结】通过这道题目我们可以看出，不定方程这类题目列式子其实并不难，难点在于求解的过程。在解不定方程的时候可以首选奇偶特性进行解题，但是有些题目通过奇偶特性不好进行求解的时候，我们可以换个解题思路，比如快速换因子特性进行解题，这样可能会事半功倍。公考路途漫漫，但是只要努力一定会有收获，最终上岸。希望本次分享能够帮助到各位同学。为了帮助大家记忆，给大家整理了思维导图。
【思维导图】
双阳华图 电话0431-8180-7290
以上就是【不定方程题型之因子特性法】的相关介绍，如果要了解更多热门资讯，欢迎关注吉林华图教育。
华图优品 
助你上岸
招考资讯
图书教材
