2021-09-29 11:37:55 吉林公务员考试网 jl.huatu.com 文章来源:华图教育
2022国考行测数量关系之巧解不定方程
百鸡问题说:“鸡翁一,直钱五,鸡母一,直钱三,鸡雏三,直钱一。百钱买百鸡,问鸡翁、母、雏各几何?”。设x,y,z分别表示鸡翁、母、雏的个数,则此问题即为求不定方程组的非负整数解x,y,z,这是一个不定方程组的问题。
在数量关系中,有些考生在解不定方程时往往不知如何下手,其实不定方程的相关知识和方法并不复杂,今天我们就一起来梳理一下。

![]()
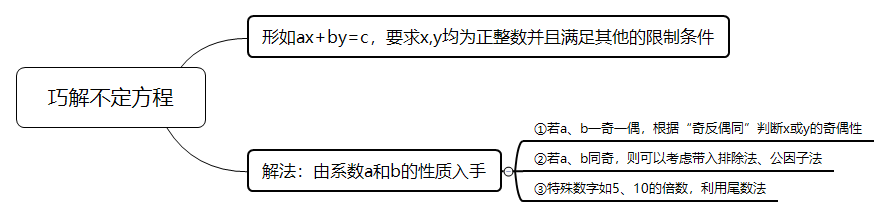
不定方程是指形如“ax+by=c”的方程,其中a,b为系数,像这种未知数个数多于方程个数的方程叫做不定方程。如3x+4y=16就是不定方程,这种方程的解是不确定的。如果不加限制的话,它的解有无数组,但如果附加一些限制条件的话,就会使得这个方程仅有唯一解是满足条件的,如3x+4y=16的解有&x=1&y=3.25,&x=2&y=2.5,⋯。如果限定x,y为不超过5的正整数,那么解就只有&x=4&y=1这一组了。因此,研究不定方程主要就是分析讨论这些限制条件对解的影响。此类方程的解法可从系数a,b的奇偶性入手,具体而言可分为两种情况:
![]()
①若a,b一奇一偶,则可以考虑奇偶性,根据“奇反偶同”判断x或y的奇偶性解不定方程;
![]()
②若a,b同为奇数,则可以考虑公因子法、带入排除法或特殊数字如5、10的倍数利用尾数法解不定方程。
下面我们就以几道例题来进行详细讲解:
【例1】某班有56名学生,每人都参加了a、b、c、d、e五个兴趣班中的其中一个。已知有27人参加a兴趣班,参加b兴趣班的人数第二多,参加c、d兴趣班的人数相同,e兴趣班的参加人数最小,只有6人,问参加b兴趣班的学生人数有多少个?( )
A.7个 B.8个
C.9个 D.10个
【答案】C
【解析】设五个兴趣班的人数分别数a、b、c、d、e人,则可以得到 b+2c=23。显然系数为1和2即一奇一偶,23为奇数,根据奇反偶同得知 b 是奇数,排除 B、D选项,代入 A 选项,得知b=7,c=8,7<8,不满足题意,故选C。
【例2】现有5盒动画卡片,各盒卡片张数分别为:7、9、11、14、17。 卡片按图案分为米老鼠、葫芦娃、喜羊羊、灰太狼4种,每个盒内装的是同图案的卡片。已知米老鼠图案的卡片只有一盒,而喜羊羊、灰太狼图案的卡片数之和比葫芦娃图案的多1倍,那么图案为米老鼠的卡片的张数为( )
A. 7 B. 9
C. 14 D. 17
【答案】A
【解析】5盒动画卡片共有7+9+11+14+17=58(张),喜羊羊、灰太狼图案的卡片数之和比葫芦娃图案的多1倍,即是葫芦娃的2倍。那么喜羊羊+灰太狼+葫芦娃=3×葫芦娃,那么3×葫芦娃+米老鼠=58,显然系数3和1均为奇数,且无公因数,故采用带入排除的思想。代入A选项,得葫芦娃=17,米老鼠=7,代入B、C、D选项,葫芦娃的张数均得不到正整数解,故选A。
【例3】甲、乙两种笔的单价分别为7元、3元,某小学用60元钱买这两种笔作为学科竞赛一、二等奖奖品。钱恰好用完,则这两种笔最多可买的支数是( )
A.12 B.13
C.16 D.18
【答案】C
【解析】设购买甲、乙两种笔的数量分别为x,y,则7x+3y=60,在总费用一定的前提下,要使得购买数量尽可能多,即甲种笔要尽量的少,根据等式,显然系数为7和3均为奇数,“3y和60”均含有因子3,则x必然是3的倍数,则x=3,y=13,总支数是 16。故选 C。
【例4】超市将99个苹果装进两种包装盒,大包装盒每个装12个苹果,小包装盒每个装5个苹果,共用了十多个盒子刚好装完。问两种包装盒相差多少个?
A.3 B.4
C.7 D.13
【答案】D
【解析】设大、小盒子各有x、y个,由大盒每个装12个,小盒每个装5个,恰好装99个,得到12x+5y=99。根据奇偶特性,其中12x是偶数、99为奇数,故5y为奇数;显然5y为5的倍数,且尾数为5,则12x的尾数为4,可得x=2或x=7,当x=2时,y=15,符合共有十多个盒子,此时15-2=13;当x=7时,y=3,不符合共十多个盒子(刚好十个)。故两种包装盒相差 13个,选择 D选项。
以上就是关于不定方程的求解问题,小伙伴们是不是发现并没有如大家想象的那么复杂呢,其实对于不定方程来说,知识点还是很容易理解的,只要大家勤学多练,对于所讲的求解方法灵活运用,熟能生巧,一定会掌握的游刃有余。
以上就是【2022国考行测数量关系之巧解不定方程】的相关介绍,如果要了解更多热门资讯,欢迎关注吉林华图教育。

贴心微信客服