2021-08-30 13:13:38 国家公务员考试网 jl.huatu.com 文章来源:吉林华图
2022年国家公务员行测备考技巧:几何问题中相似定理的应用
不管是公务员还是事业单位考试,数量关系对于绝大多数考生来说是一大难点,特别是几何问题。对于几何问题考查的重点主要分成三个部分:第一个部分是基本公式类、第二个部分是几何特性、第三个部分是几何构造。而近几年来考查的方向主要趋向于几何特性部分,今天我们就来聊聊几何特性部分中的三角形相似的应用。
何为相似?
相似指相类、相像的意思。语出《易·系辞上》:"与天地相似,故不违。"学科上解释:如果两个图形形状相同,但大小不一定相等,那么这两个图形相似。
三角形相似
定义:三角分别相等,三边成比例的两个三角形叫做相似三角形。
基本定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
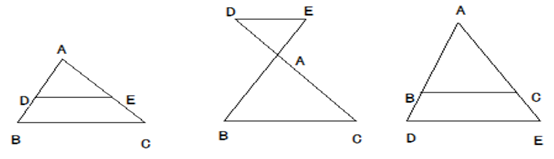
![]()
即:
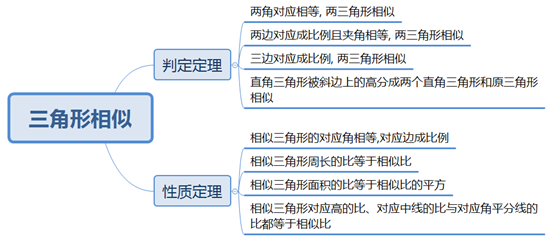
判定定理和性质定理
| 判定定理 | 性质定理 |
| 两角对应相等, 两三角形相似。 | 相似三角形的对应角相等,对应边成比例。 |
| 两边对应成比例且夹角相等, 两三角形相似。 | 相似三角形周长的比等于相似比。 |
| 三边对应成比例, 两三角形相似。 | 相似三角形面积的比等于相似比的平方。 |
| 直角三角形被斜边上的高分成两个直角三角形和原三角形相似。 | 相似三角形对应高的比、对应中线的比与对应角平分线的比都等于相似比。 |
通过以上对于三角形相似的定义、判定定理以及性质定理的学习,我们来看看近几年数量关系中对几何性质的考查题目。
【例题1】一块三角形农田ABC(如下图所示)被DE、EF两条道路分为三块。已知BD=2AD,CE=2AE,CF=2BF,则三角形ADE、三角形CEF和四边形BDEF的面积之比为:

A. 1∶3∶3
B. 1∶3∶4
C. 1∶4∶4
D. 1∶4∶5
【答案】C
【解析】第一步,本题考查几何问题,属于几何特性类。
![]()
第二步,根据题意知,BD=2AD,CE=2AE,CF=2BF。得、。根据三角形相似的判定定理:两边对应成比例且夹角相等, 两三角形相似。即,再根据三角形相似的性质定理:相似三角形面积的比等于相似比的平方,得三角形ADE和三角形ABC面积之比为1:9,因此三角形ABC的面积为9的倍数,即三角形ADE、三角形CEF和四边形BDEF的面积和为9的倍数。
因此,选择C选项。
【例题2】如下图,某植物园四边形花圃ABCD的面积为90,EC:AE=5:4,则三角形花圃BCD的面积是多少?
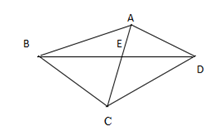
A. 40
B. 50
C. 60
D. 65
【答案】B
【解析】第一步,本题考查几何问题,属于几何特性类。
![]()
第二步,根据题意,做三角形 ABD 的高 AF 交 BD 于 F,做三角形 BCD 的高 CG 交 BD 于 G,则直角三角形 AFE 和直角三角形 CGE 相似,则对应边成比例,所以 AF:CG=4:5,三角形 ABD 和三角形 BCD 同底,所以对应高的比等于面积比=4:5,则三角形 BCD的面积=。
因此,选择B选项。
通过这些题目,我们不难看出,无论题目形式如何多变,但是内涵本质不变。在备考阶段遇到几何问题中涉及三角形时,应用三角形相似的性质做题,不仅会缩短做题的时间,还会提高效率。
以上就是【2022年国家公务员行测备考技巧:几何问题中相似定理的应用】的相关内容,如果要了解更多国家公务员行测备考技巧相关内容,欢迎关注吉林华图教育。

贴心微信客服