2021-08-03 08:47:02 国家公务员考试网 jl.huatu.com 文章来源:吉林华图
2022国考行测备考干货之奇偶特性
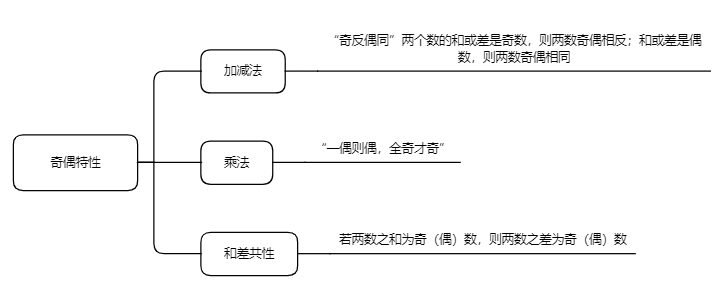
数字特性是我们做题时比较容易忽略的,但是很多时候我们又可以利用数字特征来快速的解决数量关系题。今天就要给大家介绍一种常见的数字特性——奇偶特性。奇偶特性,其实就是一个数是奇数还是偶数。先说偶数,何为偶数?能被2整除的数是偶数,或者说以“0”、“2”、“4”、“6”、“8”结尾的数就是偶数。反过来,不能被2整除的就是奇数。
奇数与偶数之间运算存在一些性质,例如奇数±奇数=偶数,奇数±偶数=奇数,奇数×奇数=奇数,等等。我们可以利用这些性质来快速的解决问题。下面我们先来看一道例题。
【例题】方程px+q=99的解为x=1,p、q均为质数,则p×q的值为:
A.194 B.197
C.135 D.155
【答案】A
【解析】第一步,由于x=1是该方程的解,那么我们将其代入方程可以使等式成立,即得到p+q=99。
第二步,p、q为质数,p、q的和是99是个奇数,那么p、q中一定是一个奇数一个偶数。又由于所有的质数(大于1的自然数中只能被1和自身整除的数)中只有“2”这一个偶数。所以p、q分别是2和97。
第三步,p×q=2×97=194。因此,答案选择A选项。
其实这题到第二步判断出p和q是一奇一偶,就可以选出答案了,一个奇数乘以一个偶数一定是个偶数,选项中四个数只有A选项是偶数,所以此题选A选项。
由上题可以看出,有时候直接利用选项的奇偶特性就可以快速判断出答案,可以进一步提高做题速度。接下来我们再看一道题。
【例题】某年级有4个班,不算甲班其余三个班的总人数有131人,不算丁班其余三个班的总人数是134人;乙、丙两班的总人数比甲、丁两班的总人数少1人,问这四个班共有多少人?
A.177 B.176
C.266 D.265
【答案】A
【解析】第一步,根据题干可知我们需要求的是甲班、乙班、丙班、丁班总人数。设这四个班的人数分别是甲、乙、丙、丁。
第二步,根据题干条件可以得到以下式子

显然这里有甲、乙、丙、丁4个未知数,但是却只有3个方程,不可能把4个未知数都求出来。但是题目只要求我们求一个式子即:甲+乙+丙+丁。
第三步,通过观察③式不难发现,如果把乙丙当做一个整体,甲丁当做一个整体。它们的奇偶性质是不一样的,本题所求甲+乙+丙+丁就是一奇一偶两个数相加,那么结果一定是个奇数。此时剩下的答案就只有A、D两个了。D答案是题干中2个数的和,明显超过四个班总人数。所以答案只有A选项了。当然这题也可以利用方程将乙+丙,甲,丁分别求出来,再求和,也可以得到答案A。
相信通过以上两个题大家对奇偶特性的应用有了初步的了解。在这里需要提醒大家的是,我们做题时很容易忽略掉有这种方法可以运用,大家不要忘了还有奇偶特性可以利用哦。
【知识总结】
以上就是【2022国考行测备考干货之奇偶特性】的相关内容,如果要了解更多公务员考试,公务员行测相关内容,欢迎关注吉林华图教育。

贴心微信客服
下一篇:没有了