2021-08-02 11:49:50 吉林公务员考试网 jl.huatu.com 文章来源:净月华图
2022年国考行测数资均值不等式的函数题目应用
均值不等式是行测数资经常会考查的对象,这个知识点也经常会运用到实际生活中,但在理解上存在难度,所以我们遇到这类考察题目时,总是拿捏不到考点,造成失分或者白白浪费了宝贵的思考时间。下面我们就通过一道题目具体讲讲这些思想方法是如何切入函数题目的。
【例题】
某苗木公司准备出售一批苗木,如果每株以4元出售,可卖出20万株,若苗木单价每提高0.4元,就会少卖10000株,问在最佳定价的情况下,该公司最大收入是多少万元?
A.60 B.80
C.90 D.100
【解析】
第一步,确认本题考查最值问题。
第二步,结合题目信息,“每株以4元出售,可卖出20万株”,得出是多件商品问题求总收入的最值,只能使用总收入=单株收入×株树的方程列式。根据信息“苗木单价每提高0.4元,就会少卖10000株”,假定提高了n个0.4元时,总收入取得最大值。
第三步,列式得到:(4+0.4n)×(20-n),变化一下形式,将0.4提公因子,得到0.4×(10+n)×(20-n),运用均值不等式原理,使10+n=20-n,解得n=5,将n=5代入原式中,得到(4+0.4×5)×(20-5)=90。
因此,本题选择C选项。
【总结】
这类题有多种解法,我们一一对比一下,再看看为什么一定让大家坚决学会均值不等式的原理解决本题。
解法一:当列出了(4+0.4n)×(20-n)式子后,存在一个很大的问题,此式子是一元二次方程所形成的一元二次函数求最值。很多同学忘记了怎么处理一元二次函数。可考虑反向思维,使用代入排除,因为实际情况下,提价应该不会提得太高,可考虑将n=1、2、3、4……,依次代入,这是没有办法的办法。
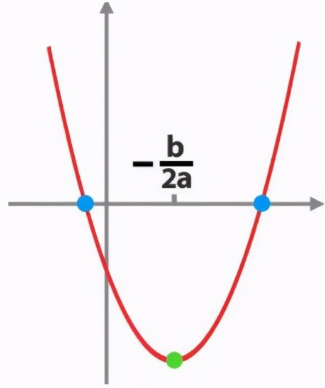
解法二:对于很多初中函数基础打得较好的人,可能会立刻想到利用二次函数y=ax2+bx+c最值问题的数形结合求解。如下图所示:
![]()
将(4+0.4n)×(20-n)变换成-0.4n2+4n+80,将a=-0.4、b=4代入-亦可解得。

解法三:利用数形结合以及二次函数的对称性,令y=0.4×(10+n)×(20-n),解得n=-10和20,在函数图形上找到n=-10和20的中点,也可解得。
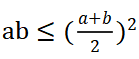
解法四:根据均值不等式原理:针对,满足“一正、二定、三相等,积定和最小,和定积最大”。一正表示a、b均为正值,二定表示a+b的和为定值,三相等表示当a=b时,可取得最值。将这个原理运用在这种题目中的思维方式是,将式子0.4×(10+n)×(20-n)中的(10+n)引申为a,(20-n)引申为b,就可以解释上述解法了。
曾经的考题中,这种函数题目在经济利润、几何问题等题目中都有考查,当明白了这个引申的思维,以后遇到类似的题目就会很快得出答案的。
【思维导图】
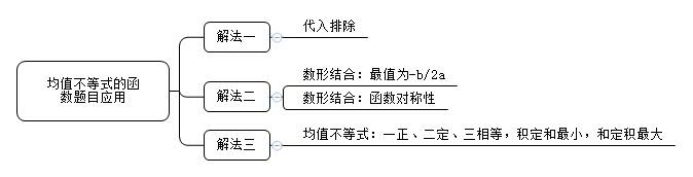
以上就是【2022年国考行测数资均值不等式的函数题目应用】的相关介绍,如果要了解更多热门资讯,欢迎关注吉林华图教育。

贴心微信客服
下一篇:没有了