国考问题-几何最值问题浅谈

国考问题-几何最值问题浅谈

　　几何问题几乎是每次行政职业能力测试的必考内容，通常来讲常规的几何问题一般难度都不大，只要大家掌握常见的几何定理，几何计算公式都较容易解决。但是关于几何问题偶尔会考到一些与最值相关的题目，这些题目比较讲求技巧性。今天我就给大家简单介绍一下部分几何最值问题求解的思路。

　　我们知道在平面图形当中，如果一个图形的周长一定，则这个图形的形状越接近于圆其面积越大。

　　其形式我们可以想象成一群小朋友在上体育课，按照老师的要求，所有小朋友手拉手围成一圈，那么这一圈的周长就是所有小朋友臂展的加和。刚开始时，大家聚集在一起，胳膊没有完全伸展开，中间围起来的空地面积会相对较小。随着老师口令，大家逐渐向后退，中间的空地会越来越大，但这一过程中大家手一直拉在一起，整个队伍的周长一直是所有小朋友臂展的加和。直到大家的胳膊完全伸展开，此时队伍会呈现一个很标准的圆形，中间的空地面积达到最大。如果再大，大家就没法保持手拉手状态了。

　　其形式我们可以想象成一群小朋友在上体育课，按照老师的要求，所有小朋友手拉手围成一圈，那么这一圈的周长就是所有小朋友臂展的加和。刚开始时，大家聚集在一起，胳膊没有完全伸展开，中间围起来的空地面积会相对较小。随着老师口令，大家逐渐向后退，中间的空地会越来越大，但这一过程中大家手一直拉在一起，整个队伍的周长一直是所有小朋友臂展的加和。直到大家的胳膊完全伸展开，此时队伍会呈现一个很标准的圆形，中间的空地面积达到最大。如果再大，大家就没法保持手拉手状态了。

　　根据这一条几何最值理论，考试时便可以设计一道几何最值的题目，比如：

　　【例1】某健身馆准备将一块周长为100米的长方形区域划为瑜伽场地，将一块周长为160米的长方形区域划为游泳场馆。若瑜伽场地和游泳场馆均是满足周长条件下的最大面积，问两块场地面积之差为多少平方米?

　　A. 625

　　B. 845

　　C. 975

　　D. 1150

　　在本题中，瑜伽场地为周长为100米的长方形区域，题目需要求得瑜伽场地的最大面积。根据上面的几何最值理论，此问题符合周长一定的前提条件，所以当这块区域为正方形时面积最大，即如下图1所示，正方形的边长应为25米，其面积为625平方米。

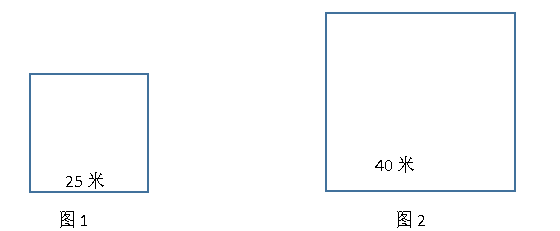
　　同理，游泳馆场地为周长为160米的长方形区域，当这块区域为正方形时面积最大，即如上图2所示，正方形的边长应为40米，其面积为1600平方米。

　　所以，两块场地面积之差为1600-625=975平方米，选择C选项。

　　如果我们仅仅理解到此题的程度，只能算是形式上理解了这条最值理论。实际应用这条理论具体计算题目时，核心的计算方法依据的是如果两个数的和一定，那么当两个数相等时候这两个数的积最大。表示成算式就是如果X+Y=M，(X，Y，M均为正数)，当X=Y=M2时，XY取得最大值。

　　比如上题中的瑜伽场地，如果我们设他的长为a、宽为b，有(a+b)×2=100米，a+b=50米，最大面积即为ab的最大值，只有当a=b=25米时，ab取得最值，ab=25×25=625平方米。

　　所以在解题时要注意结合以上两种思路来检验自己的解题方法是否准确。

　　比如：

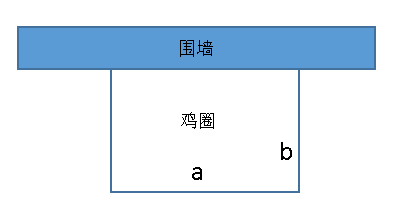
　　【例2】某农家要建造一个新的矩形鸡圈，如图所示，该鸡圈一面靠围墙，另外三面共使用了200米长的铁丝网，问如果想让鸡圈的面积最大，鸡圈的长和宽比值应为多少?

　　A. 1∶1

　　B. 2∶1

　　C. 3∶2

　　D. 7∶3

　　在求解本题时，如果大家不理解上面我们说的第二种思路，便会误认为鸡圈为正方形时面积最大，实际上本题的情况并不满足周长一定。因为随着鸡圈长宽的变化，利用的围墙长度也在变化。如按图中所示，应该是a+2b=200米，除围墙外三边的总长度是固定的。

　　正确的方法应该按第二种思路处理，如果a与2b的和一定，当a=2b=时，a×2b最大，则a×b也最大。所以，a：b=2：1，B选项是正确答案。

　　希望通过这样两个例题详细解释，能够给大家关于几何最值问题的学习提供必要帮助。

以上就是【国考问题-几何最值问题浅谈】的相关介绍，如果要了解更多热门资讯，欢迎关注吉林华图教育。