2022国考行测数量关系:巧做最值问题

2022国考行测数量关系:巧做最值问题

　　数量关系中有一种题型叫最值问题，它分为最不利构造、数列构造、多集合反向构造三种小题型。这种题型如果不用技巧，直接利用枚举或其它方式做的时候很难快速解题，这里给大家分享一下最常考的两种最值问题的题型特点以及计算方法。

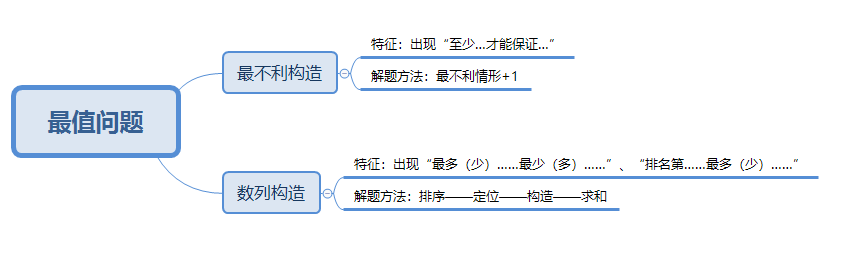
　　最不利构造

　　题型判定：题目中出现“至少…才能保证…”

　　解题方法：最不利情形：即保证值-1;如果部分值<保证值-1时，直接照抄计算即可

　　答案=“最不利情形+1”

　　【例1】(2020深圳)某演唱会主办方为观众准备了白红橙黄绿蓝紫7种颜色的荧光棒各若干只，每名观众可在入口处任意选取2只，若每种颜色的荧光棒都足够多，那么至少( )名观众中，一定有两人选取的荧光棒颜色完全相同。

　　A.14 B.22

　　C.28 D.29

　　【解析】第一步，根据题目最后出现特征“至少…才能保证…”，确定本题考查最不利构造。

　　第二步，找到最不利情形是要保证值-1，即2-1=1人，那最不利的情形就是每个人选取的荧光棒都不完全相同，即若观众选取的是2支同色的荧光棒有=7(种)方式，若观众选取的是2支不同颜色的荧光棒有= 21(种)方式，共有7+21=28(种)方式。答案应为“最不利情形+1”，即至少有28+1=29(名)观众才能保证一定有两人选取的荧光棒颜色完全相同。

　　因此，选择D选项。

　　【例2】(2019重庆)某地区招聘卫生人才，共接到600份不同求职者的简历。其中，临床、口腔、公共卫生和护理专业分别有200人、160人、140人和100人，问至少有多少人被录用，才能保证一定有140名被录用者专业相同?

　　A.141 B.240

　　C.379 D.518

　　【解析】第一步，根据题目最后出现特征“至少…才能保证…”，确定本题考查最不利构造。

　　第二步，要保证140名录用者专业相同，则最不利的情形是只有140-1=139名满足，则所有的最不利情形=139+139+139+100=517(名)，则所求=517+1=518(名)。即至少有518人录用，才能保证一定有140名录用者专业相同。

　　因此，选择D选项。

　　数列构造

　　题型判定：题目特征：出现“最多(少)……最少(多)……”、“排名第……最多(少)……”

　　解题方法：排序——定位——构造——求和

　　【例1】(2021广东)某街道服务中心的80名职工通过相互投票选出6名年度优秀职工，每人都只投一票，最终A、B、C、D、E、F这6人当选。已知A票数最多，共获得20张选票;B、C两人的票数相同，并列第2;D、E两人票数也相同，并列第3;F获得10张选票，排在第4。那么B、C获得的选票最多为( )张。

　　A.11 B.12

　　C.13 D.14

　　【解析】第一步，本题考查最值问题，属于数列构造。

　　第二步，80人共投出80张票，若使得B、C获得的选票最多，则A、D、E、F票数尽量少。已知A票数最多，共获得20张选票，F获得10张选票;因此尽量让D、E的票数最少，且高于F，均是11票。

　　第三步，B、C共获得最多票数为80-20-10-11×2=28(张)，B、C两人的票数相同，则B=C=28÷2=14(张)。

　　因此，选择D选项。

　　【例2】(2019江西)某高校计划招聘81名博士,拟分配到13个不同的院系,假定院系A分得的博士人数比其他院系都多,那么院系A分得的博士人数至少有多少名?

　　A.6B.7

　　C.8D.9

　　【解析】第一步，本题考查最值问题中的数列构造问题。

　　第二步，总共招聘81名博士，要想院系A分得的博士数最少，则应构造其余院系分得的博士数尽可能多。设院系A分得博士x名，那么其余12个院系最多均有x-1名，可列方程：x+(x-1)×12=81，解得x≈7.2，那么院系A分得的博士至少有8名。

　　因此，选择C选项。

　　注意：在审题的过程中要注意区分最多和都多，还要注意是否可以有相同的情况。

　　更多资讯请关注辉南华图微信客服(HNHT19969533096),咨询地址：吉林省辉南县通化市辉南县朝阳镇二建东50米华图教育，辉南华图近期课程咨询电话：0435-8256679。

以上就是【2022国考行测数量关系:巧做最值问题】的相关介绍，如果要了解更多热门资讯，欢迎关注吉林华图教育。