2022国考工程问题的核心技巧

2022国考工程问题的核心技巧

　　很多备考的考生在国考备考过程中，反映数量关系模块时间紧难度大，打算舍弃这个模块，其实这是非常不明智的做法，我们应当在数量关系模块中挑选好拿分的题型，比如工程问题，相对于考生而言，好掌握且难度不大，因此在这篇文章中我们重点给大家分析工程问题的核心技巧。

　　(1)认识工程问题

　　工程问题实际是一类干活类问题，常见的题目表现形式有“工程队”“修路”“水池放水”等，但是更为核心的工程问题在于三量关系，工作总量、工作效率以及工作时间，工作时间也就是我们所说的干活所用的时分秒，比如“完成一项工程需要20天”，这种表述就是工作时间，工作总量就是所有的活，比如“要修2100千米的路”。工作效率反映的是单位时间的工作量，比如“甲每天折10个飞机”。

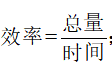
　　工程问题中核心的公式就是工作总量=工作效率×工作时间，考生只要牢牢抓住这三量关系，就能就行题目的计算和求解，例如要求解工作效率就可以利用题目的设计无外乎一项工程、两项工程，甲乙两个工程队，或者涉及人力50个人割麦子。

　　(2)工程问题的核心技巧

　　下面我们将通过两道题目来给大家介绍工程问题的核心技巧，其实在中学阶段，我们所接触到的工程问题，其核心技巧是默认工作总量为1，那么工作效率就是分之一的一个数值。其实这种思想就是工程问题解题的核心技巧，赋值法，顾名思义就是给未知的量假设一个特定的值，但是要求这个值不影响最终的结果。

　　【例1】(2017年国考副省级)工厂有5条效率不同的生产线。某个生产项目如果任选3条生产线一起加工，最快需要6天整，最慢需要12天整;5条生产线一起加工，则需要5天整。问如果所有生产线的产能都扩大一倍，任选2条生产线一起加工最多需要多少天完成?

　　A.11 B.13

　　C.15 D.30

　　【解析】第一步，本题考查工程问题，属于时间类，用赋值法解题。

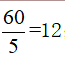
　　第二步，赋值总量为60，则全部五条的效率为最快的三条生产线效率和为得到最慢的两条生产线的效率和为12-10=2。

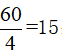
　　第三步，利用扩大一倍，得到现在的两条生产线效率和为4，则时间为

　　因此，选择C选项。

　　【例2】(2015年国考副省级)某农场有36台收割机，要收割完所有的麦子需要14天时间。现收割了7天后增加4台收割机，并通过技术改造使每台机器的效率提升5%。问收割完所有的麦子还需要几天?

　　A.3 B.4

　　C.5 D.6

　　【解析】第一步，本题考查基础应用题。

　　第二步，赋值每台收割机的效率为1，得到现有36+4=40(台)，提升后等效为40×(1+5%)=42(台)。

　　第三步，设还需要t天，可得：36×14=36×7+42×t，解得t=6。

　　因此，选择D选项。

　　通过这两道题，我们不难看出，在工程题解题过程中，我们可以赋值工作总量为时间的公倍数，一般是最小公倍数，大大减轻了我们计算的难度，从而提高了我们解题速度和效率，同时我们在涉及到人力的题目中，默认的每人干相同的活，效率是一样的，那么我们可以通过赋值效率为1，来达到简化计算的目标。

　　(3)固定模型之牛吃草

　　(2019年联考)某河道由于淤泥堆积影响到船只航行安全，现由工程队使用挖沙机进行清淤工作，清淤时上游河水又会带来新的泥沙。若使用1台挖沙机300天可完成清淤工作，使用2台挖沙机100天可完成清淤工作。为了尽快让河道恢复使用，上级部门要求工程队25天内完成河道的全部清淤工作，那么工程队至少要有多少台挖沙机同时工作?

　　A.4 B.5

　　C.6 D.7

　　【解析】第一步，本题考查牛吃草问题，用公式法解题。

　　第二步，设河道原来的淤泥堆积量为y，每天上游河水带来新的淤泥量为x，根据牛吃草问题公式：y=(n-x)×t，可列方程组：;解得x=0.5，y=150。

　　第三步，设要想25天内完成清淤工作至少需要n台挖沙机，可列方程：解得n=6.5，即至少需要7台挖沙机。

　　因此，选择D选项。

　　这类牛吃草问题的本质实际还是工程问题，源自工程最早的模型水池放水问题，只要抓住一个核心，其中默认每头牛每天的吃草效率为1，其中核心等式为总的草量为长的草量加上牛吃的草。

以上就是【2022国考工程问题的核心技巧】的相关内容，如果要了解更多公务员行测,公务员考试相关内容，欢迎关注吉林华图教育。