2022吉林公务员行测备考：巧用因子特性解不定方程

2022吉林公务员行测备考：巧用因子特性解不定方程

　　数量关系在我们行测的备考中至关重要，俗话说“得数量者得行测”，我们在备考的过程中往往发现有些模块学习起来既简单又好上手，这就要求我们在数量学习的过程中要有选择性，其中不定方程在考试中属于一个高频考点，而且它的知识点通俗易懂，是大家备考过程中的一个必会考点，其中因子特性用来解不定方程可以快速的选出答案，下来就将用因子特性解不定方程的方法给大家予以讲解：

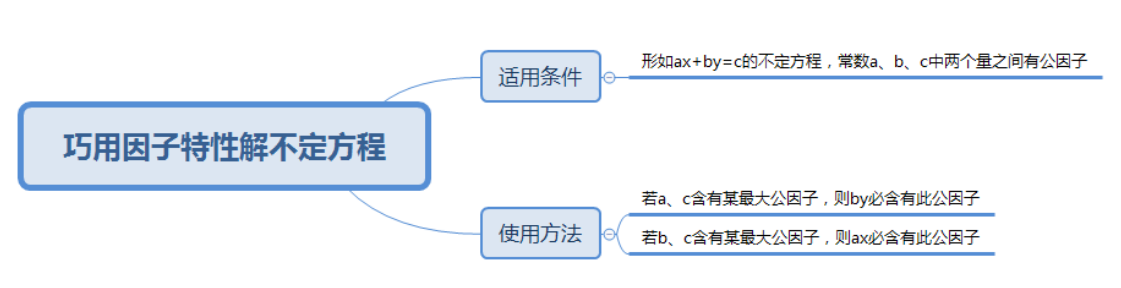
　　【因子特性知识点】

　　在ax+by=c类不定方程中，若其中两项都含有某因子，则剩余的一项必有该因子。

　　其中一项含有某因子，另外一项不含该因子，则剩余一项一定含有该因子。

　　【例1】(2017年山东)小张的孩子出生的月份乘以29，出生的日期乘以24，所得的两个乘积加起来刚好等于900。问孩子出生在哪一季度?

　　A. 第一季度

　　B. 第二季度

　　C. 第三季度

　　D. 第四季度

　　【答案】D

　　【分析】分析题干，设出生月份为x，出生日期为y。根据题意可得：29x+24y=900。由于24与900都能被12整除，根据因子特性可知：29x也能被12整除，故x必能被12整除。因x表示月份，故只能为12月份，即第四季度。

　　因此，选择D选项。

　　【例2】(2020陕西)某水果经销商到一山区水果基地采购猕猴桃和苹果。猕猴桃和苹果的采购价分别为10元/斤和4元/斤，销售价分别为25元/斤和12元/斤。已知该经销商在本次经销中获利40000元，每种水果采购都超过500斤且为整数。问该经销商的最佳投入资金是多少元?

　　A.20000

　　B.21260

　　C.21300

　　D.21280

　　【答案】B

　　【分析】分析题干，设猕猴桃、苹果分别购买的重量为x斤、y斤，由题意可得：(25-10)x+(12-4)y=40000，化简为15x+8y=40000。由于8y与40000都能被8整除，根据因子特性可知：x为8的倍数，又因x要最少(投入最少)且大于500，则x=504，y=4055。则最佳投入为504×10+4055×4=21260(元)。

　　因此，选择B选项。

　　【例3】(2020四川)某人花400元购买了若干盒樱桃。已知甲、乙、丙三个品种的樱桃单价分别为28元/盒、32元/盒和33元/盒，问他最多购买了多少盒丙品种的樱桃?

　　A.3

　　B.4

　　C.5

　　D.6

　　【答案】B

　　【分析】分析题干，设甲、乙、丙三个品种分别购买了x、y、z盒，那么由题意有28x+32y+33z=400。由于盒数都是正整数且28x、32y、400都是4的倍数，根据因子特性可知：33z必然是4的倍数，即z是4的倍数，只有B符合题意。

　　因此，选择B选项。

　　以上就是用因子特性解不定方程的方法，大家在平时的学习中要正确列出不定方程的算式，记住我们的解题思路，在做题时认真仔细，就能拿到我们数量关系中宝贵的2分，希望大家下来多多练习，能尽早掌握次解题方法!

　　【思维导图】

以上就是【2022吉林公务员行测备考：巧用因子特性解不定方程】的相关介绍，如果要了解更多热门资讯，欢迎关注吉林华图教育。