2024年公务员考试行测数量排列组合之隔板法

在数量关系这一模块题目中，排列组合相对于考生来说犹如炼狱一般，在备考刷题或者是考试的时候，面对这一类型的题目大多数考生都会由于畏难情绪选择放弃，去做其他类型的题目，事实上这类型题目的确需要利用严谨的数学思维，且根据题目研究给定要求中的排列或组合可能会出现的情况数。但接触过公务员考试或者是有过系统备考复习经验的同学肯定了解，排列组合当中我们会学到审题方法能更好的理解题目，同时运用排列组合的一些技巧，帮助我们能够更快更准确地求解题目。下面我们先来梳理一下学到的解题技巧。

在学习排列组合之初，我们学到了什么是排列组合和计算方法，清楚了基本概念，接下来又学习到了分类和分步的加法和乘法原理串联多个排列组合关系，最后我们学习了一些排列组合的解题技巧，如：捆绑法、插空法、隔板法、环形排列等。下面我们就隔板法进行深入分析。

【题型特征】

将M个相同的元素分给N个不同的主体，保证每个主体至少分配到1个元素，有多少种不同的分配方法。

【原理分析】

我们先通过一个简单的小例子来了解其原理。现在有6个相同的糖果要分给4位小朋友，要求每位小朋友至少分1个，有多少种分法?

思考：要将6个糖果分成4个小朋友，也就是要将6个糖果分成4份，并且要求有1份至少有1个，也就是用板子把横排6个糖果分隔成4份，怎么隔呢?我们来看下面这个图：

如图中所示，在6个糖果之间，形成了5个空隙，找3个空隙，用板子隔出来，就可以将6个糖果分为4份，且保证至少有小朋友至少分到1个糖果。具体是用排列还是用组合呢?我们发现糖果都是一样的，所以不需要考虑顺序，故用组合，从5个空中选择3个插入隔板，将其分为4份，满足题意，则有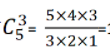=10种。我们发现，所以在排列组合中遇到将M个相同元素分给N不同的主体，每个主体至少分配1个元素，就可以用求解了。清楚基本原理之后我们通过具体题目来进行应用。

【例1】某城市一条道路上有4个十字路口，每个十字路口至少有一名交通协管员，现将8个协管员名额分配到这4个路口，则每个路口协管员名额的分配方案有：

A.35种B.70种

C.96种D.114种

【解析】

第一步：题干中给出了这样几个信息：①题目最后设问描述“分配方案”有多少种，故为排列组合类型题目;②题干中说到将8个协管员名额分配到4个路口，因为分配的是交通协管员名额，则说明8个元素是一样的，并无差异，每个路口至少有一名交通协管员。符合排列组合中隔板法题目特征。

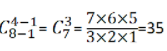第二步：根据隔板法解题方法，代入可得种。

因此，选择D选项。

【例2】某单位订阅了30份学习资料发放给3个部门，每个部门至少发放9份材料，问共有多少种不同的发放方法?

A.7种B.8种

C.12种D.10种

【解析】

第一步：题干中给出了这样几个信息：①题目最后设问描述“发放方法”有多少种，故为排列组合类型题目;②题干中说到30份学习资料发放给3个部门，每个部门至少发放9份学习资料。从题干描述中看起来不符合排列组合中隔板法题目特征，但是做一个转化之后，就可以使用隔板法解题。

第二步：要使用隔板法技巧解题，就要先将题目转化为先给3个部门每个部门发放8份，剩余材料每个部门至少发放1份则符合隔板法特征。先发放38=24份，剩余6份学习资料发放给3个部门，每个部门至少发放一个，可使用隔板法公式。

第三步：根据隔板法解题方法，代入可得种。

因此，选择D选项。

图书推荐