2023-08-29 18:53:37 国家公务员考试网 jl.huatu.com 文章来源:吉林华图
公务员考试行测数量关系:一元二次函数求极值
只要掌握常用的解题方法,拿下这类题型就并不难,甚至还会觉得很简单。那今天就来带大家一起学习。
一、一元二次函数表达式
![]()
二、解题方法
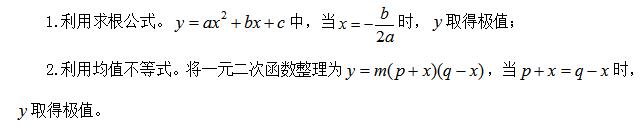
三、例题应用
例1
某商品的进货单价为80元,销售单价为100元,每天可售出120件。已知销售单价每降低1元,每天可多售出20件。若要实现该商品的销售利润最大化,则销售单价应降低的金额是:
A.5元 B.6元 C.7元 D.8元
【解析】C。方法一,设应降低x元,总利润为W元,则降低后的销售单价为(100-x元,销量为(120+20x)件。此时总利润W =(100-x-80)(120+20x)。当W=0 时,解得x的两个值分别为x=20,x=-6,根据一元二次函数图像性质,当x=(20-6)-2=7时w最大。故本题选C。
方法二,设应降低x元,总利润为平元,则降低后的销售单价为 (100-x)元,销量为(120+20x)件。此时总利润W =(100-x-80)(120+20x)= 20(20-x)(6+x)。根据均值不等式原理,当20-x=6+x,即x=7时,W取最大值。故本题选C。
例2
北京冬奥会期间,冬奥会吉祥物“冰墩墩”纪念品十分畅销。销售期间某商家发现,进价为每个40元的“冰墩墩”,当售价定为44元时,每天可售出300个,售价每上涨1元,每天销量减少10个。现商家决定提价销售,若要使销售利润达到最大,则售价应为:
A.51元 B.52元 C.54元 D.57元
【解析】D。方法一,设售价上涨x元,每天销量减少10x个,单日利润为了元。售价上涨前每个“冰墩墩”利润为44-40=4元,售价上涨后每个“冰墩墩”利润为(4+x)元,每天销量为(300-10x)个。根据单日利润=单个利润X每日销量,有y=(4+x)(300-10x)。当y为0时,x的两个值分别为x=-4,x,=30,根据一元二次函数图像性质,当x=(-4+30)-2=13时,y最大,此时售价为 44+13=57元。故本题选D。方法二,设售价上涨x元,每天销量减少10x个,单日利润为了元。售价上涨前每个“冰墩墩”利润为44-40=4元,售价上涨后每个“冰墩墩”利润为(4x)元,每天销量为(300-10x)个。根据单日利润=单个利润X每日销量,有y=(4+x)(300-10x)=y=10(4+x)(30-x)。根据均值不等式原理,当4+x= 30-x,即x=13时,y最大,此时售价为 44+13=57元。故本题选D。
通过以上题目的练习,相信大家已经认识到了这类题型的解题思路较为固定。平时可以多加练习,进一步巩固。
以上就是【公务员考试行测数量关系:一元二次函数求极值】的相关内容,如果要了解更多公务员考试行测数量关系:一元二次函数求极值相关内容,欢迎关注吉林华图教育。

贴心微信客服
下一篇:没有了