2023年国考行测备考干货：数量关系中十字交叉法的运用

2023年国考行测备考干货：数量关系中十字交叉法的运用

　　十字交叉法，即进行二组混合物平均量与组分计算的一种简便方法。凡可按Aa+Bb=(A+B)r计算的问题，均可按十字交叉法计算。式中，r表示某混合物的平均量，a.b则表示两组分对应的量。如r表示被混合后整体的平均价格，a.b则表示两组分各自的平均价格，A.B表示两组分在混合物中所占的数额，A∶B在大多数情况下表示两组分的对应数量之比。

　　在公务员考试中，这种思维方式的运用并不少见，例如我们在做数量关系亦或资料分析的部分题目时，如果题干本身存在两部分量混合得到整体的情形，就可以运用十字交叉法快速构建题干中关于A∶B的比例关系，利于解题。本文将重点阐述在国考行测数量关系中对十字交叉法的运用。那么，十字交叉法在数量关系解题中它是什么?十字交叉法的适用条件是什么?接下来本文将给大家进行详细的解答。

　　1.十字交叉法是什么:

　　十字交叉法其实是表达含未知数等式的一个工具，那这个工具如何推演出来的呢?

　　【例】有两杯葡萄糖水，假设编号为①的葡萄糖水总量为A，葡萄糖浓度为a;编号为②的葡萄糖水总量为B，葡萄糖浓度为b(a>b);问，将两杯葡萄糖水混合倒入编号为③的杯中，此时葡萄糖的浓度为多少?

　　【解】假设③杯中混合的葡萄糖浓度为r;我们可以得到以下推论：

　　(1)根据溶质守恒，我们可知混合后葡萄糖质量不变，溶质=溶液总量×浓度;

　　(2)①②杯中葡萄糖水总量=③杯中葡萄糖水总量;

　　(3)③杯中葡萄糖浓度r应该介于①②杯浓度a、b之间，即a>r>b;

　　由以上三个推论我们可构建如下等量关系：

　　Aa+Bb=(A+B)r

　　Aa-A×r=B×r-Bb

　　A×(a-r)=B×(r-b)

　　最后推得的，我们用十字交叉法这个工具来表示即可，接下来我们来探讨如何使用十字交叉法。

　　2.十字交叉法的使用方法:

　　(1)混合值用十字交叉法表示(用较大数减去较小数);

　　加和值为最终求得的比值关系;

　　3.例题分析

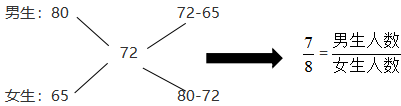
　　【例1】在环保知识竞赛中，男选手的平均分为80分，女选手的平均分为65分，全部选手的平均得分为72分，问男女人数之比?

　　【分析】

　　(1)全班人数=男生人数+女生人数(加和关系);

　　(2)全班平均分介于男、女生平均分之间(混合关系);

　　由以上两点分析可以去构建本题关于Aa+Bb=(A+B)r的等式，即:

　　男生人数×男生平均分+女生人数×女生平均分=(男生人数+女生人数)×全班平均分;

　　用十字交叉法快速求解可得如下，

　　【例2】【19浙江】小张去年底获得一笔总额不超过5万的奖金，她将其中的60%用来储蓄，剩下的用来购买理财产品，一年后这笔奖金增值了5%。已知储蓄的奖金增值了3.3%，问购买理财产品的奖金增值了多少?

　　A.5.35% B.6.45%

　　C.7.55% D.8.65%

　　【分析】C

　　(1)奖金总额=用于理财金额+用于储蓄金额(加和关系);

　　(2)理财增值率、储蓄增值率与奖金增值率(混合关系);

　　由以上两点分析可以去构建本题关于Aa+Bb=(A+B)r的等式，即:

　　用于理财金额×理财增值率+用于储蓄金额×储蓄增值率

　　=奖金总额×奖金增值率=(用于理财金额+用于储蓄金额)×奖金增值率;

　　用十字交叉法快速求解可得如下，

　　a=7.55%

　　因此选择C选项。

　　【例3】【例9】【16联考】某高校艺术学院分音乐系和美术系两个系别，已知学院男生人数占总人数的30%，且音乐系男女生人数之比为1∶3，美术系男女生人数之比为2∶3，问音乐系和美术系的总人数之比为多少?

　　A.5∶2 B.5∶1

　　C.3∶1 D.2∶1

　　【分析】D

　　(1)学院男生=音乐系男生+美术系男生(加和关系);

　　(2)音乐系男生占比、美术系男生占比与学院男生占比(混合关系);

　　(3)音乐系男生占比=1∶4=25%

　　美术系男生占比=2∶5=40%

　　由以上两点分析可以去构建本题关于Aa+Bb=(A+B)r的等式，即:

　　音乐系人数×音乐系男生+美术系人数×美术系男生

　　=学院人数×学院男生占比=(音乐系人数+美术系人数)×学院男生占比

　　用十字交叉法快速求解可得如下，

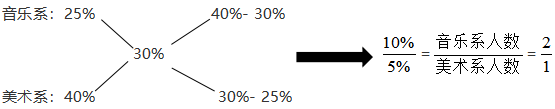
　　因此选择D选项。

　　结合上述三个例题，我们不难发现在满足使用十字交叉法的条件时，我们可以考虑灵活运用简化其计算。大家在以后的练习过程中，遇到类似的题目，多应用十字交叉法，总结思路，举一反三。通过大量的训练，相信大家一定能在数量关系版块有一个质的提升。

以上就是【2023年国考行测备考干货：数量关系中十字交叉法的运用】的相关内容，如果要了解更多国考行测备考干货,数量关系中十字交叉法运用相关内容，欢迎关注吉林华图教育。