2022-04-22 11:46:05 国家公务员考试网 jl.huatu.com 文章来源:吉林华图
公务员考试行测数量关系:巧用均值不等式求极值
在行测考试中部分题型需要极值,大家往往看到“极大值”“极小值”之后就开始打退堂鼓,甚至想直接放弃开始下一题。其实只要是题型分析到位,极值问题也并不难解。今天给大家介绍一下如何利用均值不等式求解极值。
什么是均值不等式
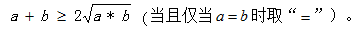
若a、b均是实数,则:
均值不等式的推论:
1.两个数的加和一定,两个数的乘积存在最大值,当且仅当两个数相等时乘积最大。
2.两个数的乘积一定,两个数的和有最小值,当且仅当两个数相等时和最小。
3.在我们考试的题目中,根据题目条件限制,有时候a与b不能取等号,这时a与b的值越接近,那么最后计算取值就会越接近最大值或最小值。
应用环境
1.题目所求极值为两数乘积的最大值,同时这两个数的加和是一个固定值时,可用均值不等式求解(需要注意区别是这两个数相等,不是两个未知数相等):
例1
老王打算用一段长为36米的篱笆围靠墙围出一个矩形的菜园,问这个矩形的长为多少米时,菜园面积最大?
A.12 B.14 C.16 D.18
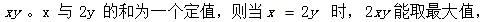
【解析】D。如下图,设矩形的长和宽分别为x米和 y米,则有,矩形的面积为
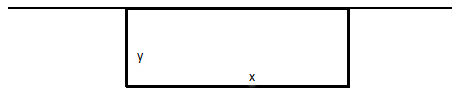

菜园面积最大。
2.题目所求极值为两数加和最大值,同时这两个数的乘积为一个固定值时也可用均值不等式求解,也需要注意区别是两个数相等,不是两个未知数相等:
例2
建造一个容积为16立方米,深为4米的长方体无盖水池,如果池底和池壁的造价分别为每平方米160元和每平方米100元,那么该水池的最低造价是多少元?
A.3980 B.3560 C.3270 D.3840
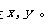
【解析】D。如下图所示,设池底的长和宽分别是则池底的面积为,池壁的面积为水池的造价为由均值不等式可知,为加和的最小值,
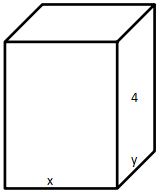
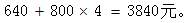
该水池的最低造价为
3.当题目条件限制,两数之间不能取等号时,则是两个数之间的取值越接近,越容易取得最大值或者最小值。
例3
沿一个平面将长、宽和高分别为8、5和3厘米的长方体切割为两部分,问两部分的表面积之和最大是多少平方厘米?
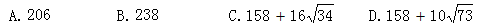
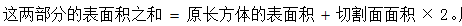
【解析】C。如下图所示,将长方体切割成两部分,则原长方体的表面积不变为要使两部分的表面积之和最大,只要切割面面积最大即可。当沿对角线切割时,面积尽可能大,这样的切割面的面积共有三种,即
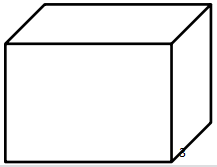
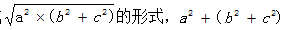
因为都可以写成的值是一定的,此时所以最大面积为
通过上述例题我们可以发现,在实际做题时能够用到均值不等式求解极值得题目,只要你能够分析出他们加和或者是乘积之间存在的定值关系,在计算时就能化繁为简,优化计算过程从而快速得到结果。
以上就是【公务员考试行测数量关系:巧用均值不等式求极值】的相关内容,如果要了解更多公务员考试行测数量关系:巧用均值不等式求极值相关内容,欢迎关注吉林华图教育。

贴心微信客服
下一篇:没有了