2022年行测数量关系干货之“工程问题”中的时间类
2022-04-12 10:59 吉林吉林选调生考试 来源:未知
2022年行测数量关系干货之“工程问题”中的时间类
根据真题数据统计,数量关系中的工程问题是联考的高频考点,近三年每年必考。其中,2021年联考考了2道,由此可见工程问题这一题型非常重要。但是,工程问题是属于重要且相对简单的题型啦,主要分为三类:时间类、效率类和条件类。今天,图图老师就带大家先来学习时间类的工程问题。
【知识要点】
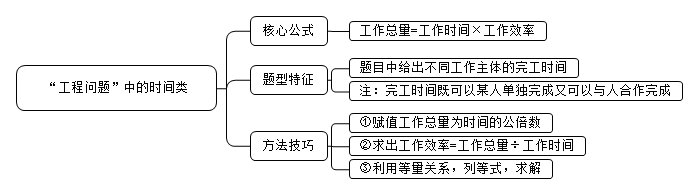
核心公式:工作总量=工作时间×工作效率
题型特征:题目中给出不同工作主体的完工时间
方法技巧:①赋值工作总量为时间的公倍数;
②求出工作效率=工作总量÷工作时间;
③利用等量关系,列等式,求解。
“给出不同工作主体的完工时间”这句话有些同学可能不太明白是啥意思,图图老师给大家举个例子,如题干信息给了“甲单独完成需要5小时,乙单独完成需要6小时”或者“甲乙合作完成需要10天,甲丙合作完成需要8天”,这些都给定的是不同工作主体的完工时间,既可以某人单独完成又可以与人合作完成。
接下来,图图老师带大家先看看入门级别的:
入门款真题:现有一批零件,甲师傅单独加工需要4小时,乙师傅单独加工需要6小时。两人一起加工这批零件的50%需要()小时。
A.0.6B.1
C.1.2D.1.5
【图图点拨】题干信息给出甲、乙两个工作主体分别的完工时间,属于时间类的工程问题。套用三步骤:①赋值工作总量为时间的公倍数:4、6的最小公倍数12(此处要注意,只要是4和6的公倍数都可以,不一定是最小公倍数,可以是12、24、36等都可以)。②求出工作效率=工作总量÷工作时间:甲的工作效率=12÷4=3,乙的工作效率=12÷6=2。③利用等量关系,列等式,求解:两人一起加工即两人合作,则甲、乙效率相加为3+2=5;两人一起加工这批零件的50%,这批零件的工作总量已经赋值为12了,根据核心公式:工作总量=工作时间×工作效率,可列式:12×50%=(3+2)×t,解方程得t=1.2小时。因此,选择C选项。
看完图图老师的点拨,同学们发现工程问题是不是非常的easy。题型识别之后套用三步骤,那咱们再来一道进阶版继续识别和套用吧~
进阶版真题:一项工程,甲一人做完需30天,甲、乙合作完成需18天,乙、丙合作完成需15天,甲、乙、丙三人共同完成该工程需:
A.10天B.12天
C.8天D.9天
【图图点拨】不管是甲单独做还是甲乙合作、乙丙合作,都属于不同主体的完工时间,属于时间类的工程问题。套用三步骤:①赋值工程总量为90(30、18、15的公倍数),则甲的效率为30÷30=1,乙、丙合作效率为30÷15=2。②甲的效率为90÷30=3,甲、乙合作效率为90÷18=5,乙、丙合作效率为90÷15=6。③甲、乙、丙三人共同完成即三人的效率相加=甲+(乙+丙)=3+6=9,根据核心公式可列式:90=(3+6)t,解得t=10天。因此,选择A选项。
【总结】
同学们,攻克下工程问题,为自己的数量关系多增添一丝信心吧!

贴心微信客服


 华图优品
华图优品  助你上岸
助你上岸 招考资讯
招考资讯 图书教材
图书教材














