2022年行测备考立体几何中“蚂蚁”与“壁虎”所引发的最短路径问题
2022-02-08 16:01 吉林公安招警考试 来源:未知
2022年行测备考立体几何中“蚂蚁”与“壁虎”所引发的最短路径问题
行测考试中,几何问题是考查频次较高的一个知识点,考查范围可能是平面几何或者立体几何。但在立体几何中,有这样一类题型,就是让一只“蚂蚁”或者“壁虎”从几何体中的某一个点到另外一个点,求蚂蚁爬行的最短距离。立体几何实际上考查的是考生的空间想象能力,看考生是否能将数形结合的思想运用于其中,解决这一类题型最有效的办法是将立体几何展开构成一个平面图形,然后再进行分析计算。那么,问题来了。请各位小伙伴思考一个问题,是否所有的路径最短问题都是拆立体几何为平面图形吗?
【例1】一只蚂蚁从右图的正方体顶点沿正方体的表面爬到正方体顶点,设正方体边长为a,问该蚂蚁爬过的最短路程为:
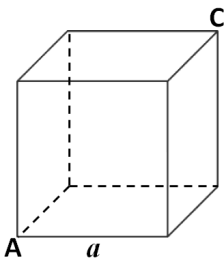
A.aB.a
C.()aD.()a
【答案】B
【解析】如下图所示,把题干中的立体几何正面展开构成平面几何,则蚂蚁所爬行的路径为AC,因“两点之间直线距离最短”,为此只需要求出AC的长度即可。因为直角三角形,为此AC==
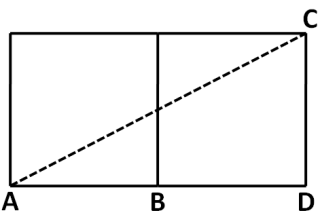
因此,选择B答案。
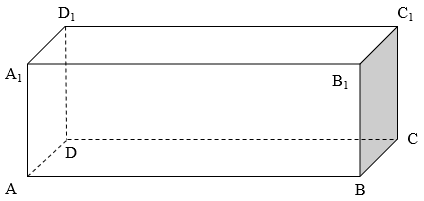
【例2】长、宽、高分别为12cm、4cm、3cm的长方体上,有一个蚂蚁从A出发沿长方体表面爬行到获取食物,其路程最小值是多少cm?
![]()
A.13B.
C.D.17
【答案】B
【解析】如下图所示,仍然将长方体展开为平面图形,根据题干所求为的长度,三角形为正方形,根据勾股定理即可求出,即=
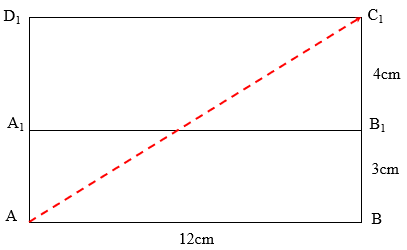
因此,选择B答案。
经过以上两个例子,不难看出,求几何体中路径最短问题,都是将立体几何拆成平面几何,然后采用勾股定理即可求出。那么,问题又来了。是不是所有的立体几何拆成平面几何以后,它所经过的行径就是最短距离呢?请接着往下看。
【例3】一个不计厚度的圆柱型无盖透明塑料桶,桶高2.5分米,底面周长为24分米,AB为底面直径。在塑料桶内壁桶底的B处有一只蚊子,此时,一只壁虎正好在塑料桶外壁的A处,则壁虎从外壁A处爬到内壁B处吃到蚊子所爬过的最短路径长约为:
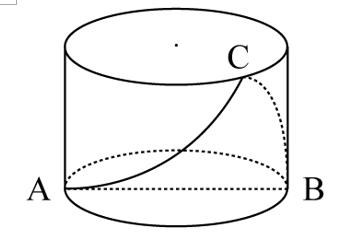
A.10.00分米B.12.25分米
C.12.64分米D.13.00分米
【答案】C
【解析】壁虎需要从外壁爬到内壁去吃蚊子,为此最短路径问题有两种情况需要考虑。
(1)情况一:圆柱侧面不展开,根据两点之间线段最短,壁虎可以先竖直走上去,然后竖直走下去,再走直径(桶是中空的),此时,走过的距离为2.5+2.5+直径(d),根据πd=24,取π≈3.14,解得d≈7.64,此时走过的最短距离为2.5+2.5+7.64=12.64(分米)。
(2)情况二:圆柱侧面展开为矩形,两点之间线段最短,我们需要将A、B两点放在同一个平面上连线即可,壁虎所经过的行径为AC+CB,现作BD的延长线DP,使得DP+BD,连接CP,此时,即CP=CB,要使得AC+CP最短,只需AC+CP最短即可。当A、C、P三点共线时距离最短,即三点都在同一直线上。为此在直角三角形ABP中,根据勾股定理,AB=12,,即AP=13分米。结合这两种情况,第一种情况距离最短。
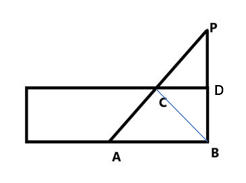
因此,选择C选项。
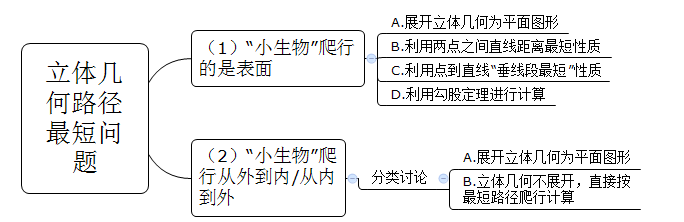
思维导图

贴心微信客服


 华图优品
华图优品  助你上岸
助你上岸 招考资讯
招考资讯 图书教材
图书教材












