2022年行测数量工程效率问题!
2022-01-12 17:24 吉林公安招警考试 来源:未知
2022年行测数量工程效率问题!
一、题型特征
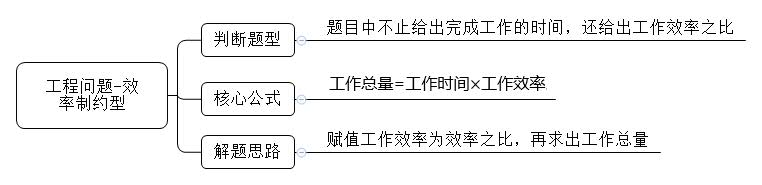
对于工程问题而言,狭义上我们一般把修桥、修路这样的基础建设工程视作工程问题,广义上,我们把“完成一件事需要多少时间”都视作工程问题,工程问题的核心公式是:工作总量=工作时间工作效率。当题目中不止给出了完成工作的时间,还给出了工作效率的比例关系的时候,就属于工程问题中的效率制约型。
【例】两工程队施工,甲乙一起施工需要9天可以完成,甲、乙两工程队的效率之比为4∶5,则若单独施工,甲需要的时间比乙多()天。
二、解题要诀
当题目中不仅给出完成工作的时间,还给出了工作效率的比例关系时,直接赋值工作效率,再求出工程总量。比如甲、乙的效率之比为2∶3,则直接赋值甲队的工作效率为2,乙队的工作效率为3。有时我们也需要观察题目,许多题目表面上没有给出工作效率之比,但是根据给出的已知信息可以推出工作效率之比,比如某题给出已知信息“A工程甲、乙、丙队合作7天可以完成,如果先由甲、乙一起干3天,再由乙丙共同干7天也可以完成。”根据次信息此信息可以得出“7甲+7乙+7丙=3甲+3乙+7乙+7丙”,也就是“4甲=3乙”,这时再使用赋值法赋值工作效率。
三、真题分享
【真题一】某市有甲、乙、丙三个工程队,工作效率比为3∶4∶5。甲队单独完成A工程需要25天,丙队单独完成B工程需要9天。现由甲队负责B工程,乙队负责A工程,而丙队先帮甲队工作若干天后转去帮助乙队工作。如希望两个工程同时开工同时竣工,则丙队要帮乙队工作多少天?()
A.6B.7
C.8D.9
【答案】B
【解析】第一步,本题考查工程问题。
第二步,赋值甲、乙、丙的效率分别为3、4、5,则由题意可得:A工程的工作总量为25×3=75;B为5×9=45。
第三步,由于两个工程开始开始并且同时完成,则总天数是(75+45)÷12=10天。A工程中,乙做10天完成工作量40,剩下35的工作量由丙完成,所以丙帮乙队做了35÷5=7天。
因此,本题选择B选项。
【真题二】一个工程的实施有甲、乙、丙和丁四个工程队供选择。已知甲、乙、丙的效率比为5:4:3,如果由丁单独实施,比由甲单独实施用时长4天,比由乙单独实施用时短5天。问四个队共同实施,多少天可以完成(不足1天的部分算1天)?
A.10B.11
C.12D.13
【答案】B
【解析】第一步,本题考查工程问题。
第二步,赋值甲乙丙的效率分别为5、4、3,由于天数有具体数值,令工程总量为5、4、3的公倍数60x,那么甲乙的天数分别为12x、15x。由丁比甲多4天,比乙少5天,可知15x-5=12x+4,解得x=3。
第三步,代入工程总量为60x,x=3,则工程总量为180,丁的时间为12x+4=40天,效率为180÷40=4.5。四队合干需要180(5+4+3+4.5)≈10.9,取整为11天。
因此,选择B选项。
通过上面两道题目的分享,相信各位考生对于工程问题中的效率制约型的题目一定有了一些收获,工程问题作为我们公考数量科目的热点之一,只要大家掌握判断题型的技巧,找出题目中所给的工作效率之比,再予以赋值,一定可以很快的解出答案。
在考公大军人数不断上涨的今日,如果再抱有陈旧的观念,放弃数量科目,那只会让自己处于不利地位,古语道:“取其上得其中,取其中得其下,取其下必败。”如果你对于数量依旧抱有恐惧的心理,不愿去学习,那它将永远是你公考路上的绊脚石。现在,就让我们大家一起从经典题型——工程问题入手,慢慢学习数量的诸多知识点吧!

贴心微信客服


 华图优品
华图优品  助你上岸
助你上岸 招考资讯
招考资讯 图书教材
图书教材












